E.m.f. generated in a rotating coil
Consider a coil of N
turns and area A being rotated at a constant angular velocity
q in a
magnetic field of flux density B, its axis being perpendicular to the field (Figure 1).
When the normal to the coil is at an angle
q to the field the flux through the coil is BAN
cos
q = BAN cos(
w)t, since
q =
wt.
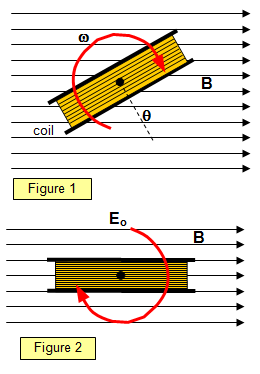
Therefore the e.m.f E generated between the ends of the coil
is:
E = -d(
f)/dt = -d(BANcos
q)/dt
Therefore:
E = BANwsin q = BANwsin(wt)
The
maximum value of the e.m.f (E
o) is when
q (=
wt) = 90
o (that is, the coil is in the plane of the field, Figure 2) and
is given by
Maximum e.m.f: Eo = BANw
At this
point the wires of the coil are cutting through the flux at right angles – they chop through the field
lines rather than slide along them.
The r.m.s. value of the e.m.f. is ERMS = BANw/[2]1/2

Example problem
Calculate the maximum value of the e.m.f generated in a coil with 200 turns and of area 10 cm2 rotating at 60 radians per second in a field of flux density 0.1 T.
E= BANw = 0.1x10-3 x 200 x 60 = 1.2 V
Notice the use of radians per second.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB