Mathematical treatment of charging and discharging a
capacitor
Discharging
The area under the current-time discharge
graph gives the charge held by the capacitor. The gradient of the charge-time graph
gives the current flowing from the capacitor at that moment.
Discharge of a
capacitor through a resistor
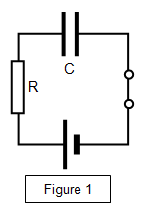
In Figure 1 let the charge on a capacitor of capacitance C at
any instant be q, and let V be the potential difference across it at that instant.
The current (I)
in the discharge at that instant is therefore:
I = - dq/dt
But V = IR and q = CV so dq/dt =
d(CV)/dt = C dV/dt
Therefore we have V = -CR dV/dt Rearranging and integrating gives:
Capacitor discharge (voltage decay): V = Voe-(t/RC)
where V
o is the initial voltage applied to
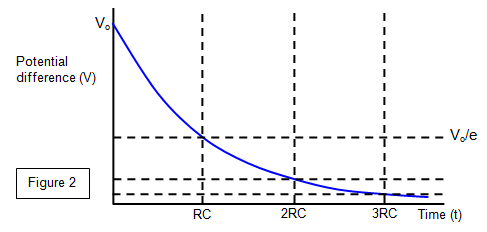
the capacitor. A graph of this exponential discharge is shown below in Figure 2.
Since Q = CV the equation for the charge (Q) on the capacitor
after a time t is therefore:
Capacitor discharge (charge decay): Q = Qoe-(t/RC)
V = Voe-(t/RC) and also I = Ioe-(t/RC) Q = Qoe-(t/RC)
You should realise that the term RC governs the rate at
which the charge on the capacitor decays.
When t = RC, V = V
o/e = 0.37 V
o and the product RC is
known as the
time constant for the circuit. The bigger the value of RC the slower the rate at which the
capacitor discharges.
The value of C can be found from this discharge curve if R is known.
Example problems
1.
A capacitor of 1000 μF is with a potential difference of 12 V across it is discharged through a 500 Ω resistor.
Calculate the voltage across the capacitor after 1.5 s
V = Voe-(t/RC) so V = 12e-1.5/[500 x 0.001] = 0.6 V
2.
A capacitor is discharged through a 10 MΩ resistor and it is found that the time constant is 200 s.
Calculate the value of the capacitor.
RC= 200
Therefore C = 200/10 x 106 = 20 μF.
3.
Calculate the time for the potential across a 100 ΨF capacitor to fall to 80 per cent of its original value if it is discharged through a 20 kΩ resistor.
V = 0.8 Vo. Therefore 0.8 = e–t/20000x0.0001
Therefore:
ln(1/0.8) = 20 000 x 0.0001
This gives t= 2xln(1/0.8) = 0.45 s.
Charging a capacitor
When a capacitor (C) is being charged through a resistance (R) to a final potential V
o
the equation giving the voltage (V) across the capacitor at any time t is given
by:
Capacitor charging (potential difference): V = Vo[1-e-(t/RC)]
and the variation of potential
with time is shown in Figure 2.

As the
capacitor charges the charging current decreases since the potential across the resistance decreases
as the potential across the capacitor increases.
Figure 4 shows how both the potential
difference across the capacitor and the charge on the plates vary with time during charging.
The charging current would be given by the gradient of the curve in Figure 2 at any time
and the graph of charging current against time is shown in Figure 3.
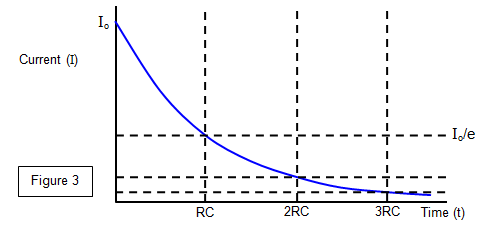
The area below the current-time curve in both charg
ing and discharging represents the total charge held by the capacitor.

Warning
Some badly made power supplies have a
capacitor connected across their outputs and so remain live even after the power supply has
been switched off. Always be careful when handling apparatus containing
capacitors.
Example problems
1. A 4000 μF capacitor is charged through a 2.5 kΩ resistor using a 15 V supply.
Calculate:
(a) the potential difference across the plates after 5s
(b) the time taken for the potential difference across the plates to reach 10 V
(a) V = Vo[1 – e-t/RC] = 15[1 – e-5/(2500x0.004)] = 5.9 V
(b) 10/15 = 1 – e-t/RC and so e-t/RC = 0.33 therefore t/RC = 1.099
This gives: t = 1.0986x2500x0.004 = 11 s
2. A 2000 μF capacitor is charged through a 1 kΩ resistor using a 6 V supply.
Calculate:
(a) the charging current after 2.5s
(b) the charge on the plates after 2.5 s
(a) Initial charging current (Io) = V/R = 6/1000 = 6 mA
Current after 2.5 s = Ioe-t/RC = 6x10-3xe-(2.5/1000x0.002) = 6x10-3 x 0.287 = 1.7 mA
(b) Q = Qo [1 - e-t/RC]
Final charge (Qo) = CV = 0.002x6 = 0.012 C
Charge after 2.5 s = 0.012[1 - 0.287] = 0.012x0.713 = 0.0086 C
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS CD