Half adder

By a small extension of the EXCLUSIVE-OR gate we can obtain a circuit that will not only add two simple binary digits but also give a carry bit.

We need a circuit where the sum bit is 0 if the two inputs are either both 0 or both 1 and where the carry bit is 1 only if both inputs are 1.

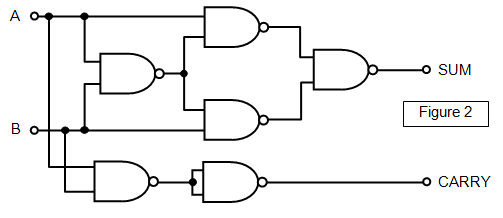
Using Boolean algebra notation and taking the inputs as A and B we can obtain the following equations for the sum bit (S) and the carry bit (C):

The sum bit (S) is given by S = A.B + A. B The carry bit (C) is given by C = A.B


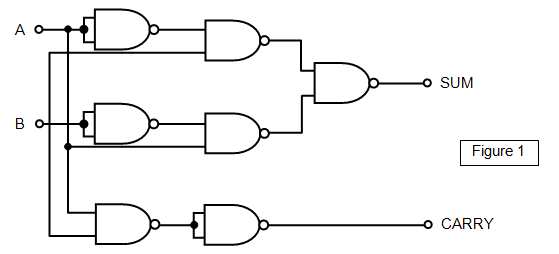
You should see that the sum bit will be given by an EXCLUSIVE-OR gate and the carry bit by an AND gate. A version of the half adder circuit is shown in Figures 1.

You should follow through the circuit checking the condition at each NAND gate to see that it produces the required output.

The truth table for the half adder is given below.

A	B	SUM	CARRY
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

An alternative version of the half adder circuit is shown in Figure 2.

Adder circuit

Using two half adders and an OR gate a full adder circuit may be produced that will add three bits A, B and C. The circuit for the full adder is shown in Figure 3.



The Boolean notation for such a circuit is:

SUM bit = A. B.C + A.B. C + A. B. C + A.B.C

CARRY bit = A.B.C + A.B. C + A. B.C + A.B.C

The truth table for the full adder is shown below.

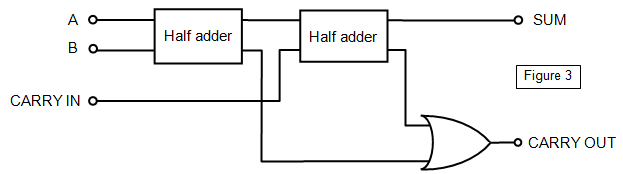
A	B	CARRY IN	SUM	CARRY OUT
0	0	0	0	0
0	1	0	1	0
1	0	0	1	0
1	1	0	0	1
0	0	1	1	0
0	1	1	0	1
1	0	1	0	1
1	1	1	1	1