The physics of long jumping

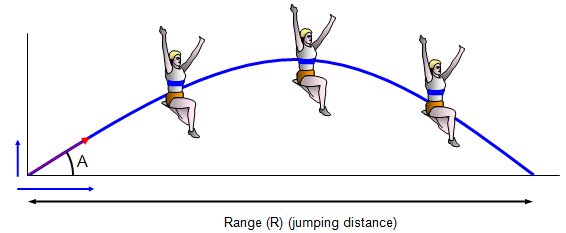
A long jumper is basically a projectile and to work out how far someone can jump we can start by looking at the motion of a simple projectile.

The projectile has two velocities – one vertically and one horizontally. To jump a long way you must run as fast as possible down the runway and then give yourself a large upward kick on take off. For a projectile, the maximum range for a given horizontal velocity is achieved for a launch angle of 45^o

However it is much easier for a long jumper to gain a large horizontal ground velocity than a large vertical velocity and so they usually have a launch angle of rather less than this.

To jump as far as possible you need a large horizontal velocity along the run up and then give yourself a vertical velocity at the take off board.

We can estimate the maximum theoretical long jump.

Let's assume a maximum horizontal velocity of 10m/s.

Range = u²sin 2A/g
So:
For A = 20^o and u = 10 m/s we have : Range = [100xsin 40]/9.8 = 6.55 m
For A = 30^o and u = 10 m/s we have : Range = [100xsin 60]/9.8 = 8.83 m
For A = 35^o and u = 10 m/s we have : Range = [100xsin 70]/9.8 = 9.58 m

If you are able to shoot your legs forward before landing you should gain an extra 0.6 m giving a total possible distance of 10.4 m.

The long jumper usually shortens their last stride so that at take off the take off leg is hitting the board at a steeper angle to give a greater upward force.

Forward rotation is a problem because at take off your body is pivoting about the take off point. To reduce this the jumper can use two techniques:
(a) a hang style or (b) the hitch kick.

In the hang style the body is kept as long as possible – a long lever will rotate more slowly for a given amount of rotational energy. In the hitch kick the legs are cycled in the opposite direction to the forward rotation of the body although this technique is only really helpful at large distances – say over about 7.5 m.

In 1991 Mike Powell of the USA set the current world long jump record for a man of 8.95m. In 1988 Galina Chistyakova of the former Soviet Union leapt 7.52 m to set the womens world long jump record. Both records still stand today (2020).