Gravitational potential gradient

The gravitational field strength (written as g or E_G) or gravitational field intensity at a point in a field is defined as the force per unit mass at that point (constant for a uniform field such as that near the surface of the Earth).

Therefore: E_G = F/m = g

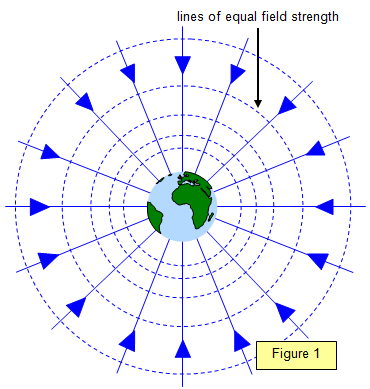
Figure 1 shows lines of equal gravitational field strength (g) around the Earth (dotted). The lines are all equally separated in terms of field strength but the radial distance between them increases as you move further from the planet. This means that there is little change in g with distance near to the Earth's surface.


The gravitational potential (V_G) at a point in a field is defined as the work done in bringing unit mass to that point from infinity.

V_G = - Gm/r

where m is the mass of the body producing the field and r is the distance from its centre. The negative sign denotes that V_G is decreasing as r increases

The change in gravitational potential (ΔV_G) is the change in energy per unit mass when it is moved from one point to another in the field.

Therefore: ΔV_G = ΔE/m

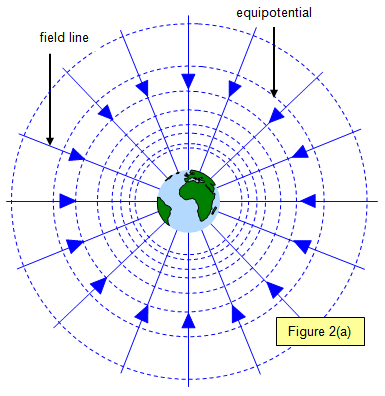
The diagram (Figure 2(a) shows lines of equipotential around the Earth (dotted). Notice that the equipotentials get further apart although the potential difference between successive lines is the same. The field lines (full lines) are at right angles to the equipotentials.


The gravitational potential gradient is defined as the rate of change of gravitational potential with distance in the field. This is equal to the gravitational field intensity (g = E_G) at that point.

Therefore: g = E_G = -ΔV_G/Δr

You should be able to see that the gravitational field strength is the same as the gravitational potential gradient.

Put simply it is the rate at which the field changes as the distance from the mass producing the field changes.

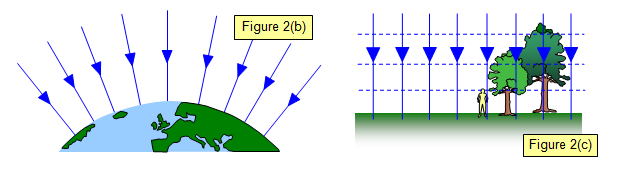
At points far from the Earth the field lines are changing their separation as the gravitational field strength (g) changes (Figure 2(b). However near the surface of the Earth the value of the gravitational field strength (g) is sensibly constant with height as long as this change of height is not too great. (See Figure 2(c))