The measurement of the focal length of a lens

Knowledge of the focal length of a lens is vital in the construction of all optical instruments, from spectacles to large astronomical telescopes. The range of possible focal lengths is very large, from a few milli- metres for the objective lens of a microscope to 20 m in a large telescope. Several simple methods are described because they all illustrate different aspects of the lens formula.

Convex lenses

(i) The focusing method
A rough guide to the focal length of a lens can be obtained by focusing light from a distant object, such as the Sun, on to a screen.



(ii) The graphical method
A graph of 1/u against 1/v can be plotted and the focal length (f) found from this. The point where the line intersects either axis is 1/f.

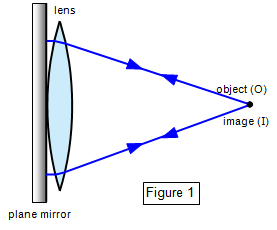(iii)

The plane mirror method
The lens is placed on the mirror as shown in Figure 1, and the object is moved until object and image coincide. This point is the principal focus, since light from it will emerge parallel from the lens and so be reflected back along its original path when it strikes the mirror. The object can be either a pin or a point source.

Since R = 2f for a lens of glass of refractive index 1.5 placed in air, the value of f can be found.

(iv) The two-position or displacement method
An illuminated object is set up in front of a lens and a focused image is formed on a screen.

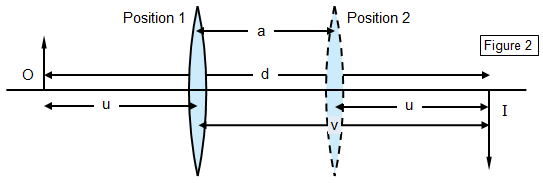
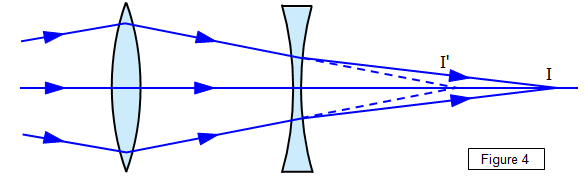
For a given separation of the object and screen it will be found that there are two positions where a clearly focused image can be formed (Figure 2). By the principle or reversibility these must be symmetrical between 0 and I.

Using the notation shown: d = u+v and a = v – u

Therefore: u = [d – a]/2 and v = [d + a]/2

Substituting in the lens equation gives:

2/[d – a] + 2/[d + a] = 1/f and hence f = [d² – a²]/4d
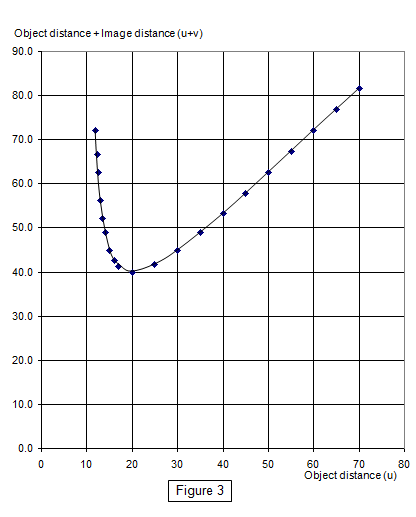
(v) The minimum distance method
This more mathematical method derives from the fact that there is a minimum separation for object and image for a given lens. This can be shown if u + v is plotted against either u or v. A minimum is formed (shown by Figure 3) and this can be shown to occur at the point where u = v = 2f and u + v = 4f, that is, the minimum separation for object and image is 4f.

Proof: 1/u + 1/v = 1/f

Therefore:
u+v = uv/f and v = fu/[u-f] so [u+v] = u/[u-f]

Differentiating the last equation with respect to u gives:

d(u+v)/du = [u²-2uf]/[u-f]²


For a minimum, d(u+v)du = 0, or u²– 2uf =0.
Therefore:

u² = 2uf or u = 2f, v = 2f, and so u + v = 4f.

Concave lenses

So far all the methods have been for convex lenses where a real image can be produced. We will now consider some methods for concave lenses.

(i) An auxiliary convex lens is used, in contact with the concave lens. It must be of greater power than the concave lens with one of its faces having the same radius of curvature as one of the faces of the concave lens. The focal length of the combination is then given by
1/F = 1/f + 1/f'
where the focal length of the convex lens f' can be found by the methods described above.

(ii) A convex lens of greater power is used to give a virtual object for the concave lens (Figure 4).

The position of this initial image (I') is found, the concave lens is then placed in position and the final image position (I) is located. The focal length of the concave lens is then found using the lens equation.

(iii) A similar method to the above can be used, replacing the convex lens with a concave mirror.