The flow of liquid through a tube

The rate at which fluid flows through a tube is likely to depend on
(a) the viscosity of the fluid,
(b) the dimensions of the tube, and
(c) the pressure difference between its ends.

This flow rate is of great importance in our lives since it governs things like the flow of blood round our bodies and the transmission of gas, water or oil through long distances in pipelines.

The proof of the relationship was first produced by Poiseuille in 1844 using dimensional analysis (a different proof based on the mechanics of fluids is available, but is outside the scope of this work at this level).

Consider a fluid of viscosity η flowing through a tube of length L and radius r due to a pressure difference Δp between its ends (Figure 1).


The formula for the rate of flow of fluid down the tube is:

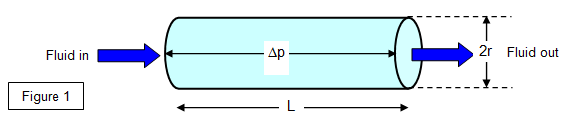
This formula only applies to laminar flow, not to turbulent motion. It is interesting that warm-blooded animals regulate the heat loss from their bodies by changing the diameter of their blood vessels (varying r) and hence controlling the rate of blood flow.

A simple proof of this formula using dimensional analysis is given below:
Assume that the volume V passing through the tube per second is given by the equation:
V = kη^xr^yDp^z/L

where the quantity Dp/L is called the pressure gradient down the tube. Using dimensional analysis this gives x = -1, y = 4 and z = 1.

Therefore the volume per second is:

Volume per second = kr4Δp/ηL

The value of k can be shown to be π/8 and therefore:

Measurement of the viscosity of a liquid

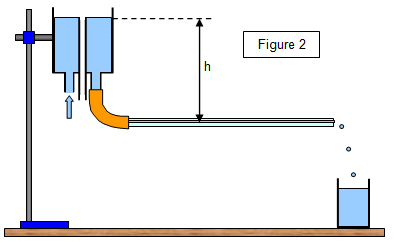
The apparatus shown in Figure 2 may be used to determine the viscosity of a liquid such as water. The water flows from a constant head apparatus through a horizontal capillary tube and is then collected by a beaker; the time for a given volume to be collected is measured. The pressure difference between the two ends of the capillary tube is hrg where r is the density of the liquid. The internal diameter of the capillary tube is measured with a travelling microscope.




It is important that the temperature of the water is measured and that the water only drips from the free end of the tube, since in the rigorous proof of the formula the water is assumed to have no residual kinetic energy. Laminar flow must also be assumed.