The efficiency of a heat engine

Any device for converting heat energy into mechanical energy is called a heat engine. Internal combustion engines and steam engines are both examples of heat engines.

A heat engine takes in heat energy at a high temperature and emits some of it at a lower temperature.

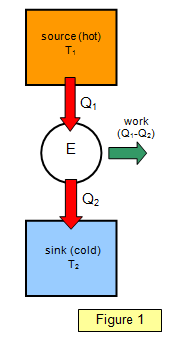
The net amount of heat flowing into an engine is equal to the net amount of work done by the engine. This can be represented by Figure 1. An amount of heat Q₁ is taken in at the higher temperature T₁ and an amount of heat Q₂ is emitted at the lower temperature T₂.

The efficiency of such a cycle is given by the equation:

Tbe concept of the ideal heat engine was first developed by the French scientist Sadi Carnot in 1824. He imagined an engine that was free from friction and where the working substance, usually a gas, was taken through a completely reversible cycle consisting of two isothermal and two adiabatic changes.

Efficiency of an ideal heat engine

The efficiency of a heat engine is defined as:

This shows that the efficiency of an ideal heat engine depends only on the temperatures of the source and sink, and also that a heat engine can never be 100 per cent efficient. For example at Dungeness power station steam at 400 ^oC (673 K) is used to drive a turbine and is emitted to the sea at 300 K. This gives a maximum efficiency of 55 per cent.

It would be useful for comparison to look up the operating conditions for some of the other nuclear power stations. The greater the operating temperature the greater the efficiency for a fixed output temperature.

The approximate efficiencies of some practical heat engines are given below:

Internal combustion engine		56%
Steam engine		40%
Diesel engine		68%
Dungeness nuclear power station		55%

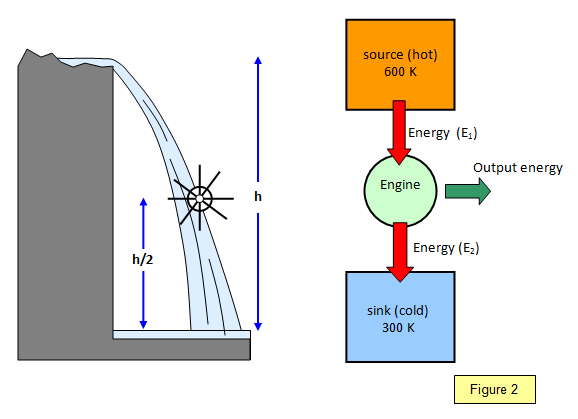
You can see how this idea works by comparing the heat engine with a waterwheel. If the waterwheel is placed half way up the waterfall then you can only expect to achieve half the energy output possible and so the efficiency would, at best, be 50%. Similarly if the heat engine was operating so that the sink temperature was half that of the source temperature then the greatest efficiency that you could hope for would again be 50%. (see Figure 2)

Note that this is the maximum possible – in practice the actual efficiency would be smaller.