
An interesting application of thermal conductivity is the calculation of the rate of growth of ice on top of a pond.
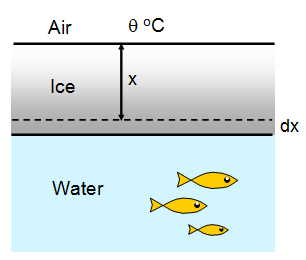
Let the air temperature be q
and the water temperature just below the ice be 0 oC.
At a certain time let the
thickness of the ice be x, and let it increase by a further thickness dx in a time dt. The latent
heat released on melting has to be conducted away through the ice layer as the water freezes
and therefore we have:
quantity of heat lost due to increase dx = rLAdx
where ρ is the density of ice, L
the specific latent heat of fusion of water and A the area of the ice surface. Then, if x is the
thickness of the ice after a time t,
rate of loss of heat = LAρdx/dt = kθA/x
Therefore dx/dt = kθ/Lρx