The Doppler Effect
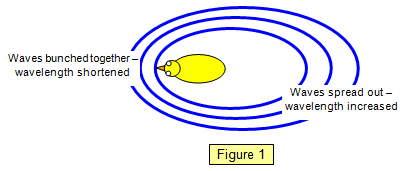
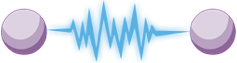
The Doppler effect is the apparent change of frequency and wavelength when a source of waves and an observer move relative to each other. These effects were first explained by Doppler in 1842 as a bunching up and a spreading out of waves. Looking at a duck swimming in a pond would show you that the waves it generates in the direction it is swimming are bunched while those behind it are spread out. (Figure 1)
In 1845 the Dutch scientist Buys Ballot tested Doppler’s theory for sound waves by using a group of trumpeters playing a calibrated note on a train on the Utrecht-Amsterdam line. They played in an open railway carriage while the carriage travelled across the Dutch countryside and observers on the ground heard a change of pitch as the carriage passed them. In fact his aim had been to disprove Doppler's theory!
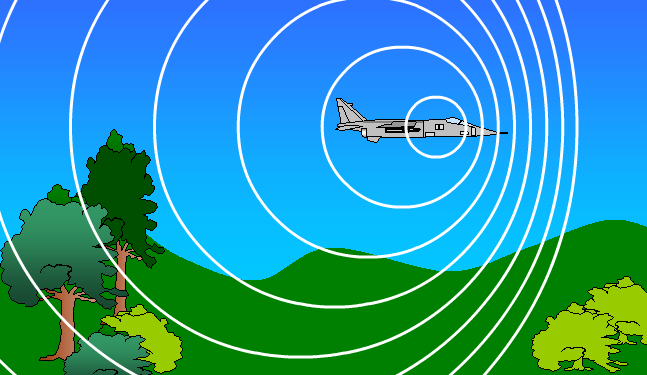
Doppler effect shown in the sound waves emitted by a fast moving jet
One of the most important applications of the Doppler effect is in the study of the expansion of the Universe. Galaxies have their light shifted towards the red due to their speed of recession and when we receive the light at the Earth we describe it as Red Shifted.
The effect can be also be observed in the following uses and applications of the Doppler effect
(a) change in the pitch of a buzzer when it is whirled around your head
(b) the change in pitch of a train hooter or whistle as it passes through a station
(c) the shift of the frequency of the light from the two sides of the solar disc due to the Sun's rotation
(d) the variation in the frequency of the light from spectroscopic binaries
(e) in police radar speed traps
(f) Doppler broadening of spectral lines in high temperature plasmas
(g) measurement of the speed of the blood in a vein or artery
We can think of a simple analogy to this by imagining that we work in a chocolate factory - packing chocolates that come to you down a steadily moving conveyor belt. (Figure 2). At the other end of the belt another person puts the chocolates on the belt at a steady rate. The chocolates therefore reach you at the same steady rate at which they were put on the belt.
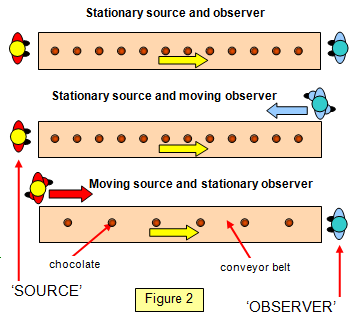
Now the other person starts to walk slowly towards you alongside the conveyor belt, still putting chocolates on at the original constant rate. You can see that you will receive the chocolates at a faster rate because after putting one chocolate on the belt your partner walks after it and when the next chocolate is put on the belt it will be closer to the first chocolate than if he or she had not moved.
You will also receive chocolates faster if you walk towards the other end of the conveyor belt collecting chocolates as you go.
Now to compare this with the transmission and reception of a wave. The rate at which the chocolates were put on the belt corresponds to the original frequency of the source, the velocity of the belt corresponds to the wave velocity (which is constant and unaffected by the motion of either the source or the observer) and the rate at which you receive them corresponds to the observed frequency.
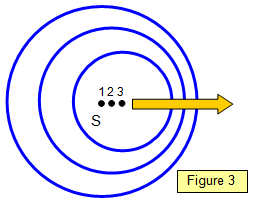
The Doppler theory in wave motion
We will now look at the Doppler effect in wave motion. Consider a source S moving from left to right. Initially it is at position 1 and some time later at positions 2 and 3. If it is emitting a wave then the three circles represent the positions of the waves emitted at points 1, 2 and 3 some time after the source passed position 3. You can see that the wavelengths on the right are closer together than those on the left; if the source is approaching an observer the wavelength will be reduced while if it is moving away they will be increased.
Proof of the formula for the Doppler effect
We will consider one case only - that of a moving source. The case for a moving observer is similar especially if the velocity of the source is small compared with the velocity of the wave.
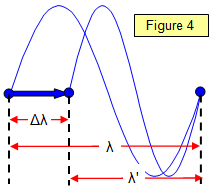
Consider a source S moving with velocity v towards an observer O, exactly one wavelength away. The source emits waves of wavelength
l, frequency f and velocity c.
In a time t the wave travels from S to O, a distance
l, and the source travels from S to S', a distance vt.
Therefore the observed wavelength
l' is
l' =
l - vt and so the wavelength change is
Dl =
l -
l' = vt but t =
l/c and so:
New wavelength (l’) = l[1 ± v/c]
and
wavelength change (Dl) = lv/c
Now since c =
lf we have:
l’ =
l [1± v/c] and so f' = f/[1 ± v/c] . Notice that an increase in wavelength gives a decrease in frequency. This equation applies to both electromagnetic radiation and to sound waves.
However providing the ratio v/c is small (say less than about 0.1) we have:
f' = f[1 -/+ v/c] , and this gives
Df = fv/c for the frequency change. Therefore for c>>v:
New frequency (f’) = f[1 -/+ v/c]
and
Frequency change (Df) = fv/c
The equations for frequency and frequency change given in the box above would only be true for situations where the speed of the waves (c) is very much greater than the speed of the source or the observer as in the case of electromagnetic radiation.
Notice that the wavelength and frequency shifts depend on the original wavelength or frequency - red light is shifted more than blue for a given velocity and that they apply whether the source or observer or both are moving.
The velocity v is the relative velocity of the source and observer as long as relativistic effects are ignored.
Doppler effect and sound
In the case of sound it is quite possible that the speed of the observer or the source is significant compared with the speed of sound.
The frequency change equation given above does not apply.
The new frequency must be calculated from: f' = f/[1 ± v/c] and then the frequency change worked out from this.
Example problems
Electromagnetic radiation
1. A galaxy is moving away from the Earth at 26000 kms-1.
Calculate the wavelength and frequency change of a 650 nm line in its spectrum. Take c = 3x108 ms-1.
Wavelength change (Dl) = lv/c = 650x26000x103/3x108 = 56.3 nm
Frequency change (Df) = fv/c = 4.6x1014x26000x103/3x108 = 0.4x1014Hz
Sound
1. Find the change in the frequency of a siren from a train that is moving towards you at 50 ms-1. Assume that the emitted frequency is 400 Hz. (Speed of sound in air = 330 ms-1)
Using :- f’ = f/[1 – v/c] = 400/[1-(50/330)] = 471.4 Hz
Therefore: Df = 71.4 Hz
2. A trumpeter plays her trumpet while in a car. The note she plays has a frequency of 300 Hz but you hear a note with a frequency of 280 Hz.
(a) is she moving towards or away from you?
(b) how fast is she moving?
(a) away – the frequency has decreased
(b) New frequency = 280 = 300/[1+v/330] Therefore: 280= (280v)/330 = 300 and so v = 23.6 ms-1
Note that in both the cases using sound the speed of the source or observer is a significant fraction of that of the speed of sound.

schoolphysics: Doppler effect animation
To see an animation of the Doppler effect click on the animation link.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB