The formula for centripetal force

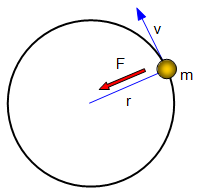
If any object of mass m is travelling round a circle of radius r at a speed of v then the force needed to keep it in this orbit is:

This formula applies to any object travelling in a circle; it gives the force needed to keep the Earth in orbit round the Sun to that needed to go round a corner on a bike.

Example problem
A motorbike and rider of total mass 100 kg travel round a roundabout of radius 8 m at a speed of 4 m/s.
What is the centripetal force needed to do this?

F = mv²/r = [100 x 4²]/8 = 200 N.

 

You should be able to see from the formula that the force needed to keep a certain object travelling at a certain speed is less when the radius of the orbit is bigger. As you would expect the faster the object goes the more force is needed to keep it in orbit.

For a given force, as the radius gets smaller the object orbits faster. Think of what happens to a stone on a string being whirled round your finger as the string winds itself up. It goes faster and faster.

Centripetal acceleration

Since F = ma the acceleration of an object moving in a circle is:

CENTRIPETAL ACCELERATION = v²/r

Example problem
A stone is whirled round on the end of a 1.5 m long piece of string. If the acceleration of the stone is 3g (30 m/s²) calculate the speed at which the stone is moving.

Use: a = v²/r so v² = ar = 30x1.5 = 45 and so v = [45]^1/2 = 6.7 m/s

Notice that the acceleration does not depend on the mass of the stone.

The stone is accelerating although its speed in the circle stays the same. The fact that it is constantly changing direction means that its velocity is changing and so it has an acceleration.

schoolphysics: Circular motion animation

To see an animation of circular motion click on the animation link.