
Objects move in a straight tine at a constant speed
unless a force acts on them. This is Newton's First Law. However, many things move in
curved paths, especially circles, and so there must be a force acting on them to pull them out
of their straight line paths and make them turn corners.
The tighter the curve that the
object is made to move in, the bigger the change of direction and so the bigger the
force.
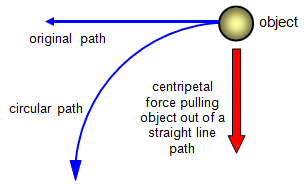
The
centripetal force always acts towards the centre of the circle to pull the object out of its
straight-line path. Although an object may travel round the circle at a constant speed its
direction of motion is always changing and so its velocity must be changing. Since a change
of velocity is an acceleration there must be a force acting on the object - the centripetal
force.
If a force acts on an object being whirled round in a circle, like a stone on the end of a string, there must be an equal and opposite force acting somewhere else. This is the centrifugal force – it acts on the ‘pivot’ at the centre of the circle. It is sometimes called a fictitious force because it does not act on the object being whirled round.
The actual way the force is produced depends on the particular
example:
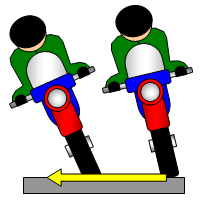
In a spin drier it is the wall of the drum pressing on the clothes. When a car,
motorbike or bicycle corners it is the friction between the wheels and the road. (You know
how difficult it is to corner on ice where there is hardly any friction.)
When the Earth orbits
the Sun it is the pull of gravity.
When a railway train corners it is the force of the rails on
the flanged wheels.
When a stone is whirled round on a string it is the tension in the
string.
What happens if we remove the centripetal force? If you are whirling a stone round your head on a piece of
string and the string suddenly breaks, which way does the stone fly off?
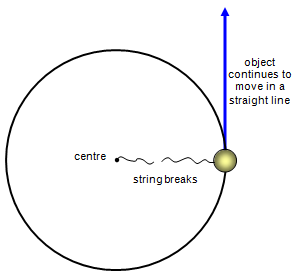
You could
try this with a soft ball instead of a stone and just let go. The ball will carry on in the direction
in which it was moving when you let go, as you ought to expect from Newton's First Law. It
DOES NOT go off along a radius of the circle.
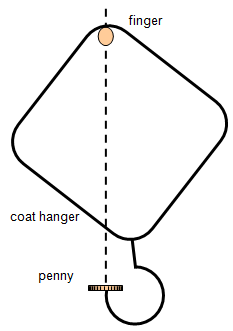
If the string wraps itself round your
finger then the stone will be moving in a circle with a smaller radius and the force will be
bigger.
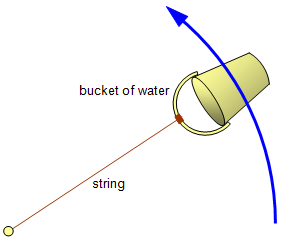
If you whirl a bucket of water around in a vertical circle you will not get wet if the speed of the bucket is great enough. At every point in the circle the water tries to fall vertically out of the bucket due to the force of gravity but also tries to move in a straight line due to its circular motion.