

As you know already, energy is always conserved but in a collision some, or all of the kinetic energy may be converted into other forms of energy such as sound and heat. In a collision between two cars a lot of the kinetic energy goes in damaging the vehicles – that's why cars have crumple zones that are designed to absorb some of this kinetic energy during a collision. There are two extreme types of collision:
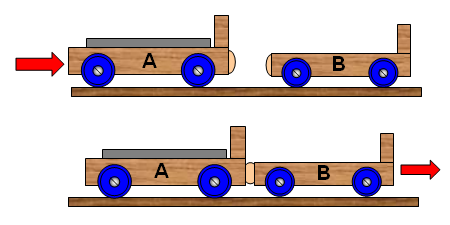
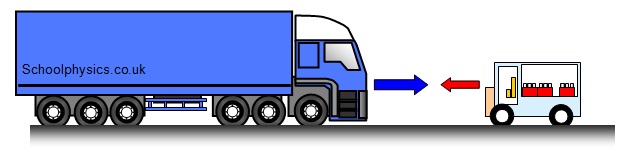
A completely elastic collision means that the two objects would simply bounce off each other when they collide (two power balls). A completely inelastic collision means that the two objects would stick together and move off as one object after the collision (two lumps of soft plasticene). If two lumps of soft plasticene of the same mass and traveling at the same speed but in opposite directions collided with each other they would stop dead – all their kinetic energy would be lost. In real life most collisions are somewhere between these two extremes. In the diagram at the top of the page a large lorry is about to collide with a small milk float. During the collision the force of the lorry on the milk float is the same as the force of the milk float on the lorry. However the effect of this force on the milk float is much greater than it is on the lorry.

The two cars in the photograph were about the same mass and travelling at roughly the
same speed when they collided. The damage to both of them was similar and they bounced
back off each other after the crash (I know – I was driving one of them!) Fortunately none of
the passengers was injured.
When two rugby players collide in a tackle some of the kinetic energy is used to deform their
bodies – the tackle hurts! When they fall over they collide with the ground – the Earth – and
this reduces their kinetic energy even more – it hurts again!
Momentum is also conserved in all collisions, and the law of conservation of momentum can be written as: