
All these facts are connected with vectors and the
addition of vectors.
Vectors are quantities that have direction as well as size. Example of
vectors are weight, force and velocity.
Quantities with no direction are called scalars and
examples of these are mass, length and energy.
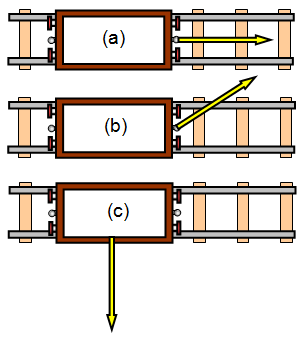
If you pull on a truck that is mounted on rails the truck will move along the
rails. However just how quickly it will move will depend not only on how hard you pull but also
on the direction in which you pull.
Obviously if you pull in the direction of the rails
the truck will move quickly (a). If you pull at an angle to the track it will move but not so
quickly (b), but if you pull at right angles to the rails (c) the truck will not move at all (unless
you actually pull it sideways off the track!).
Now imagine that you and a friend want
to pull a box along the road. (To make life easy lets imagine that the road is smooth – no
friction). The box has two ropes fixed to it and you each take hold of one of
them.
Which way should you pull?
If you both pull in the same direction
with the same force the box will accelerate quickly (d) but if you pull in opposite directions
with the same force you would expect the box to stay still and this is what would happen (e).

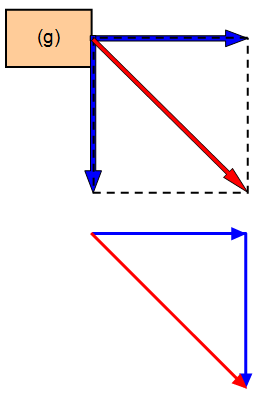
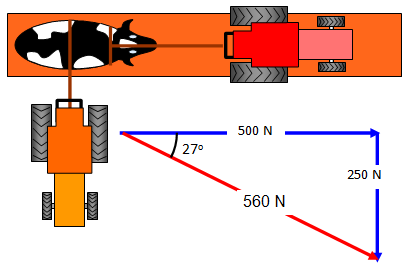 Two tractors try to rescue a cow that is trapped in a ditch. One pulls along the ditch with a force of 500 N and the other pulls at right angles to the ditch with a force of 250 N. What is the combined force on the cow and in which direction will the cow move?
Use a scale diagram showing the
two forces and the resultant.
Measuring the diagram shows that
the resultant force on the cow is just
under 560 N and that it is at an angle
of 27o with the ditch.
Two tractors try to rescue a cow that is trapped in a ditch. One pulls along the ditch with a force of 500 N and the other pulls at right angles to the ditch with a force of 250 N. What is the combined force on the cow and in which direction will the cow move?
Use a scale diagram showing the
two forces and the resultant.
Measuring the diagram shows that
the resultant force on the cow is just
under 560 N and that it is at an angle
of 27o with the ditch.
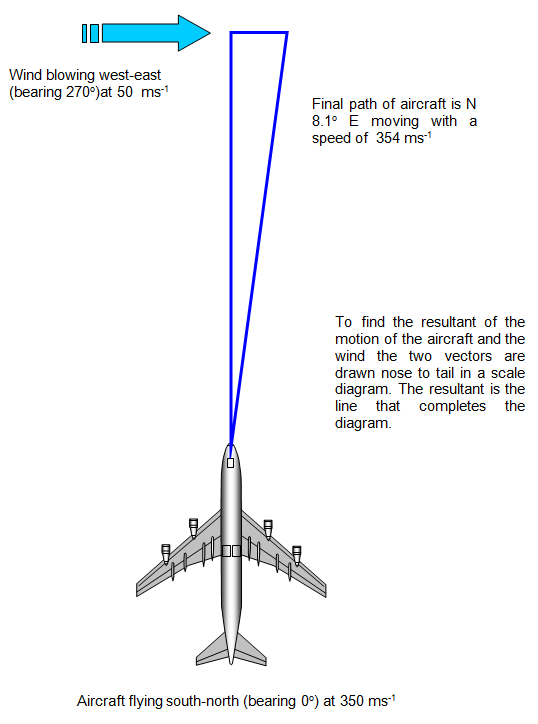
If a boat is sailing across a lake then you can
work out how long it will take if you know the speed of the boat and the distance across the
lake. This is fine if the water is still.
However what happens if the water is moving as
it is in a river. The speed of the boat compared with the bank of the river then depends not
only on its speed relative to the water but also on the sped of the water itself.
We
should really be talking about velocity here because if you remember velocity is a vector and
vectors are quantities that depend on direction as well as size.