Finding the temperatures of the stars
The Stefan-Boltzmann law gives the
total radiation emitted by the body but tells us nothing about how it is distributed across the
spectrum.

If measurements are made of the energy emitted at different temperature for a black
body then a series of curves like those shown in the diagram above can be obtained. Here the vertical axis
shows the energy density (that is the energy emitted per square metre per second in a small
wavelength range from λ to λ+dλ) and the
horizontal axis shows the wavelength.
Wien's laws and the temperatures of stars
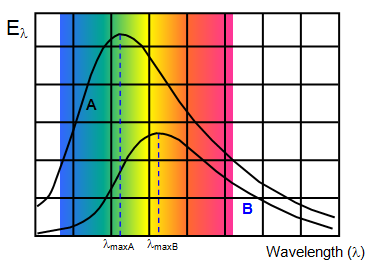
The curves in Figure 1 represent the energy output from two stars A and B. Both these stars are assumed to behave as black bodies. Star A has a higher temperature than star B and the peak of the energy-wavelength curve therfore lies further towards the shorter wavelength end of the graph.
Some important facts can be deduced from
these curves:
(a) the area between any energy-wavelength curve and the wavelength axis
gives the total energy emitted by the body per unit area at that temperature
(b) the maxima of
the curves moves towards short wavelengths at higher temperatures
(c) the curves for lower
temperatures lie completely inside those of higher temperature
It was found that:
(a) lmT = constant where λm is the wavelength at which most energy is emitted, that is at the maxima of the curves. The constant has a value of 2.898x10-3m K.
(b) the energy emitted at this wavelength (λm) is proportional to T5.
These two results are
known as
Wien's laws
| Temperature (K) |
Wavelength λm (nm) |
| 500 |
5800 |
| 750 |
3900 |
| 1000 |
3000 |
| 1750 |
1650 |
| 6000 |
480 |
| 30000 |
97 |
A range of
values for λm is shown in the table. It must be
remembered that these are for true black bodies only.
For an electric light bulb the bulb's
filament temperature (T) = 1750 K and the peak of the energy-wavelength curve (λm) is at 1400 nm.
You can see that if λm for a black body lies in the red region of the spectrum the
body will appear red hot, and as it gets hotter this peak will move towards the violet end of the
spectrum. However this does not mean that the body will look "violet hot". The reason for this is
that at the higher temperature all visible wavelengths will be present to some extent and so the
body will appear "white hot". A white-hot body will give high emission across the whole range of
the visible spectrum.
If we know the value of λm for
one black body at a known temperature we can use Wien's law to calculate the temperature of
another black body providing the wavelength at which maximum energy is emitted is known.
This
has been used extensively in astronomy for finding the temperatures of
stars.
Example problem
A black body (the Sun) with a surface temperature of 6000 K emits radiation with λm = 420 nm.
Calculate the surface temperature of Sirius (the brightest star in the northern skies) if λm for Sirius is 72 nm.
λm1T1 = lm2T2
Therefore: 420x10-9x6000 = 72x10-9xT2
Finally: Surface temperature of Sirius (T2) = 35 000 K
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB