
When X-rays pass through matter such as a
human body they will lose energy in one or more of the following ways:
(a)
Scattering – the energy of the X ray photon is not sufficient to cause electron emission from
the atom (see Compton scattering) – 1 to 30 keV
(b) The photoelectric effect - an X-
ray photon transfers all its energy to an electron which then escapes from the atom – 1 to
100 keV
(c) Compton scattering - an X-ray photon collides with a loosely-bound
outer electron. At the collision the electron gains some energy and a scattered X-ray photon
is produced travelling in a different direction from the incident photon and with a lower energy
– 0.5 to 5 MeV
(d) Pair production - an X-ray photon with an energy greater than
1.02 MeV enters the intense electric field at the nucleus. It may be converted into particles, a
positron and an electron. These two particles usually annihilate each other producing two
photons, each of energy 511 keV – above 5 MeV.
In a vacuum the intensity (I) of
the X ray beam will fall off as the inverse of the square of the distance (d) from the
source.
This is the thickness of the material which is needed to reduce the intensity (I)
of the X ray beam to one half the intensity of the incident radiation (Io).
Since : I
= Ioe-mx if I/Io = ½ then e-μx = ½ and so
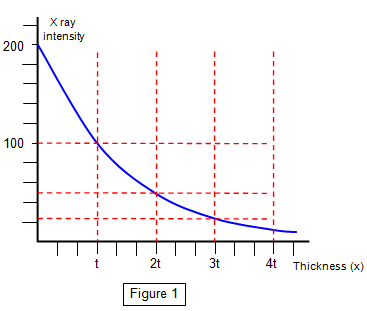
The graph shown in Figure 1 is for an X beam of one energy - monoenergetic. In this case the half value thickness of the
material is always the same no matter how much the original intensity has been reduced. If
the beam has a spread of energies then the further through the material the X ray beam
passes the longer the half value thickness becomes.
This is because the lower
energy X rays in the beam are absorbed more easily than the higher energy ones.
This
is shown in Figure 2. The X ray beam contains a greater proportion of higher energy X rays
the further into the material it penetrates. This is said to be a 'hardening' of the
beam.
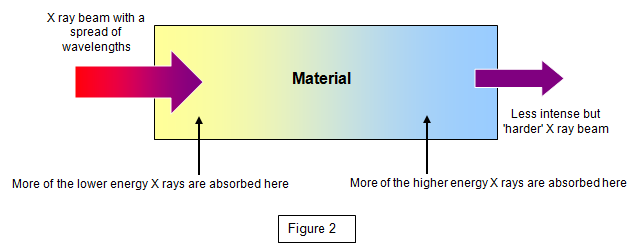
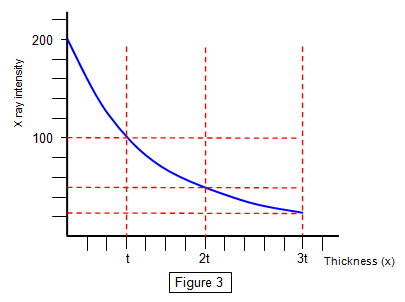
Figure 3 shows the graph for a beam of X rays with a spread of energy. It shows that the absorption curve
flattens as the beam penetrates further into the material and the half value thickness also
increases.
The equivalent energy of an X ray beam is shown by its half value thickness in a particular material. For
example X rays from an X ray tube with a peak anode voltage of 80 kV have a half value
thickness of about 3 mm of aluminium. However the half value thickness for a 28 keV
monoenergetic beam of X rays is 3 mm of aluminium and so the equivalent energy of the 80
kV X ray beam is 28 keV.
The quality of the beam is determined by the spread of X ray
energies across the spectrum.