The C-R (capacitance-resistance) circuit

The circuit shown in Figure 1 contains both resistance and capacitance, and therefore both the component and the frequency of the supply voltage affect the current in the circuit.

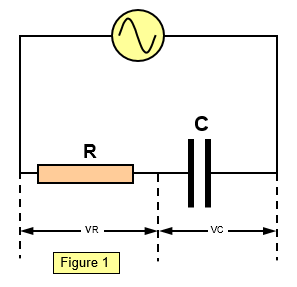
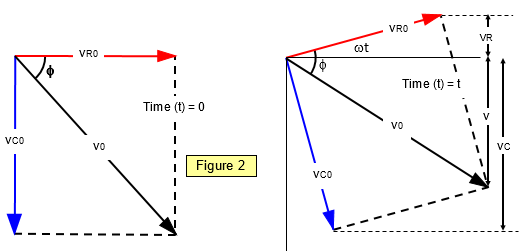
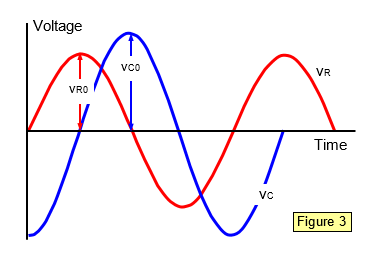
The a.c. resistance of such a circuit is known as the impedance of the circuit and is denoted by the symbol Z. Impedance is measured in ohms. We will now deduce the impedance of the circuit using the vector treatment. Consider the voltages round the circuit. The supply voltage will be denoted by Vo and the voltages across the resistor and capacitor by V_R0 and V_C0 respectively. We know that for a resistor the current and voltage are In phase, while for a capacitor the current leads the voltage by 90^o; v_R0 therefore leads v_C0 by 90^o, as shown in the vector diagram in Figure 2.

The resultant voltage v₀ is given by v₀² = v_R0² + v_C0² = i₀²R² + i₀²X²C Therefore the current in the circuit is given by:

i_o = v_o/[X_C² + R²]^1/2 and the impedance Z by:


The angle θ that the resultant vector makes with V is known as the phase angle of the voltage.

You can see from Figure 3 that tanφ = v_C0/v_R0 = -1/ωCR