
When current flows round a circuit energy is transformed in both the external resistor but also in the cell itself. All cells have a resistance of their own and we call this the internal resistance of the cell. The voltage produced by the cell is called the electromotive force or e.m.f for short and this produces a p.d across the cell and across the external resistor.
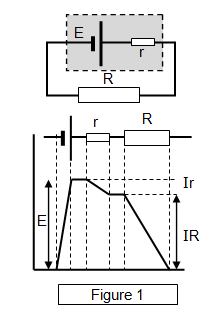
Consider the circuit shown in Figure 1. The shaded area reprsents the internal part of the cell. If the e.m.f of the cell is E and the internal resistance is r and the cell is connected to an external resistance R then:
The quantity of useful electrical energy available outside the cell is IR and Ir is the energy transformed to other forms within the cell itself.
We usually
require the internal resistance of a cell to be small to reduce the energy transformed within the cell;
however it is sometimes helpful to have a rather larger internal resistance to prevent large currents
from flowing if the cell terminals are shorted.