
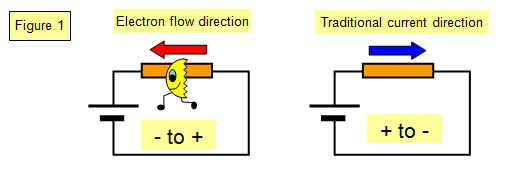
As a charge moves round a circuit from the positive to the negative it loses energy. There is a problem here. As you know an electric current is a flow of negatively charged electrons and these flow away from the negative terminal of a supply, round the circuit and back to the positive terminal. However the 'traditional' view of current flow is from positive to negative and we will take that view when looking at the energy of electrical charge.
The next set of diagrams (Figure 2) show how the potential varies round some basic circuits. To simplify the treatment we are going to assume that the energy
lost in the connecting wires is neglibgible and we are going to ignore it. This means that the energy
of the charge at one end of a connecting wire is the same as that at the other end. The bigger the
energy change the bigger the difference in potential. We call the difference in electrical potential
between two points in the circuit the potential difference between
those two places.
The potential difference between two points is defined as:
The units for potential difference are Joules per coulomb, or volts. (1
volt = 1 Joule/coulomb).
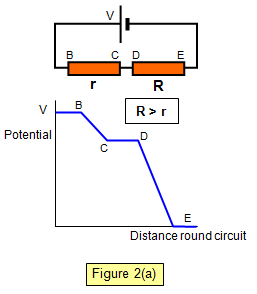
Figure 2(a) shows the variation in the potential around the circuit. We can follow this by considering each section of the circuit in
turn.
Along the connecting wire from the cell to B there is no resistance and so no loss of
electrical energy or drop in potential.
In the resistors r and R energy is converted to heat
and so the potential drops from B through to E.
From E to the cell there is no loss of
electrical energy and so the potential at E is the same as that at the negative terminal of the cell –
zero.
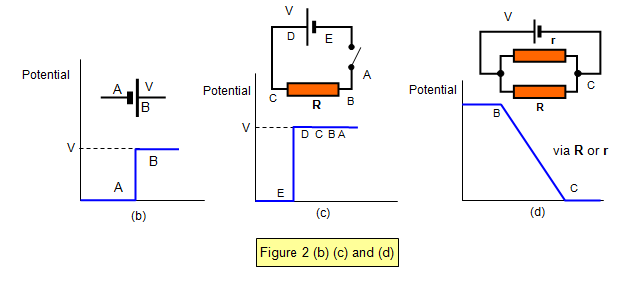
Figures 2(b and c) shows that when no current flows in a circuit there is no
change of potential and therefore no potential difference between two parts of that circuit that are
connected.