Resistance

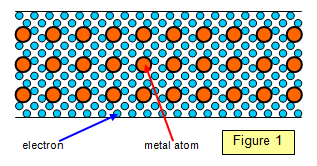
The free electrons in a metal are in constant random motion. As they move about they collide with each other and with the atoms of the metal. If a potential difference is now applied across the metal the electrons tend to move towards the positive connection. As they do so their progress is interrupted by collisions. These collisions impede their movement and this property of the material is called its resistance. If the temperature of the metal is raised the atoms vibrate more strongly and the electrons make more violent collisions with them and so the resistance of the metal increase (see later).


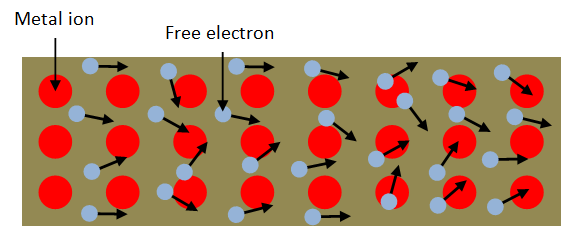
The resistance of any conducting material depends on the following factors:
(a) the material itself (actually how many free electrons there are per metre cubed)
(b) its length
(c) its cross-sectional area and (d) its temperature

The resistance of a given piece of material is connected to the current flowing through it and the potential difference between its ends by the equation:

The units of resistance are ohms (Ω).

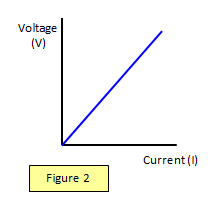
Ohm's Law

If the ratio of p.d to current remains constant for a series of different p.d.s the material is said to obey Ohm's Law. This is true for a metallic conductor at a constant temperature (see Figure 2)

This means that although we can always work out the resistance of a specimen knowing the current through it and the p.d across it. However if these quantities are altered we can only PREDICT how it will behave under these new conditions if it obeys Ohm's law.
It is also vital to realise that the resistance is simply the ratio of the voltage and current at a particular point and NOT generally the gradient of the VI curve.
It is important to realise that Ohm's Law only holds for a metallic conductor if the temperature is constant.

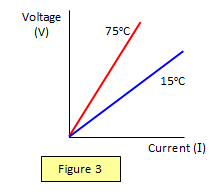
This means that if the temperature of the metal is held steady at say 15^o C the variation of current and voltage will be linear. However if the temperature of the metal changes (as in the filament of a light bulb) then the resistance will also change. The collisions between the electrons and the atoms will occur more often and be more violent.



So if the wire is raised to 75^o C a second set of readings can be taken – they will still be linear but the resistance of the wire (the ratio of V to I) will be greater (see Figure 3).

It is worth having a look at two graphs that show how the resistance of two types of material change when their temperature is changed.
The first is a metal wire (Figure 4(a)), and the second is a (negative temperature coefficient) thermistor (Figure 4 (b).

In the case of the metal wire the resistance increases as the temperature increases, you can see this because the ration of pairs of points on the V-I graph increases at high currents (hot wires). In the case of the thermistor the resistance decreases as the temperature increases, you can see because the ratio of pairs of points on the V-I graph decreases at high currents (high temperatures.).

Although the gradients of the graphs suggests a change in resistance do not be tempted to use the gradient to work out the resistance, you must still deal with the voltage/current ratio only.

The reason that the thermistor decreases is because the thermistor is a semiconductor and more free electrons are produced as the temperature is raised.

(In fact more electrons are raised to the conduction band of the material.)

Electron theory of resistance

We can consider the electrons in a solid to have a random motion similar to a cloud of gas molecules.

An electric field of intensity F is placed across a length L of the conductor. Let the conductor be of resistivity r and resistance R, and have n conduction electrons per unit volume.
The electric field (E) across the conductor is given by E = V/L and therefore Ee = Ve/L = F
where F is the force on the electron.
Using Newton's second law of motion the acceleration of an electron due to this field is then given by:

acceleration = Ve/mL

where m is the electron mass.
If the time between electron collisions is t, then (Figure 5) the velocity v' just before a collision is
v' = Vet /Lm


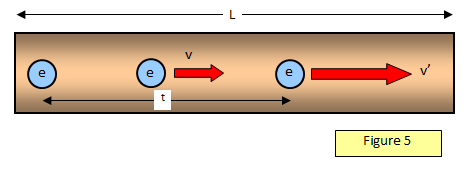
The average velocity between collisions is therefore Vet = v, but since I = nAve we have:

I = e²tnAV/2Lm

and this gives for the resistance:


If we consider the thermal velocity of the electrons to be around 10⁶ ms^-1 then the time between collisions in copper is 5x10^-14 s and the distance travelled is some 5x10^-8 m, much greater than the interatomic spacing which is about 2 x 10^-10m.

See also:
Resistivity
and:
Series and parallel resistors