Resistance networks

1. The cube

Twelve resistors in the form of a cube. The problem is to find the resistance (R) between the points A and B on each cube. Each arm of the cube has a resistance r.

There are three possible connections.
(a) We can take any path through the network between the points A and B. Such a path could be ACDB.



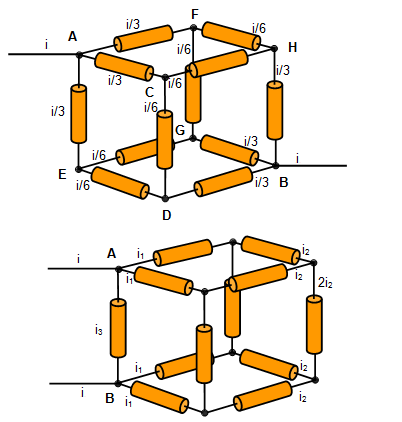
IR = i/3 r + i/6 r + i/3 r = I 5/6 r
Therefore:



Total resistance (R) = 5/6 r








(b) By symmetry

i₁ = 5i₂
i₃ = 14 i₂
i = 24 i₂

Therefore:

Total resistance (R) = 7/12 r




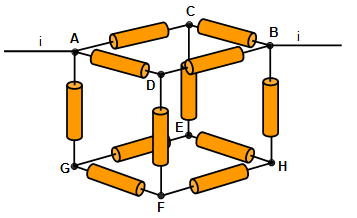
(c)
By symmetry
Potential at C = potential at D
Potential at E = potential at F
Potential at C = potential at D = potential at E = potential at F
Therefore there is no current in CE or DF

The resistance of the faces ACBD and GEHF each have a resistance r
The resistance from A to B along the path A to face GEHF to B is 3r

Therefore resistance from A to B (R) is given by:

1/R = 1/r + 1/3r = [4/3]r R = [3/4]r

2. The infinite chain

The problem here is to find the resistance (R) due to the infinite chain of resistors each of resistance r connected as shown.





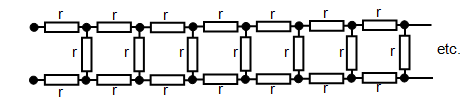
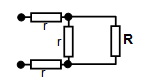
Since the chain is infinite we can think of it as being equivalent to the following circuit:

Therefore:

R = 2r + rR/[r + R] = 2.732r