The parallel-plate capacitor
In its most basic form a capacitor is simply two metal plates with a
material of permittivity
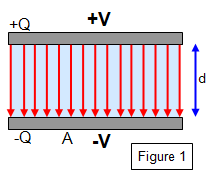
e filling the space between them shown in Figure 1. Such an arrangement is
called a parallel plate capacitor. The plates of a charged parallel capacitor each carry charges of the
same size but of opposite sign.
These charges generally spread evenly over the
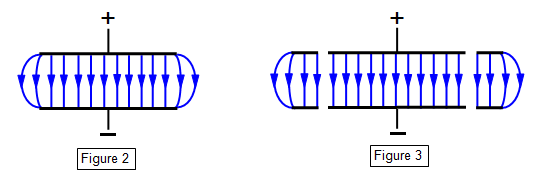
surfaces of the plates but there is a build up of charge at the sharp edges of each plate. The effect of
this on the field between the plates is shown on Figure 2. This effect can be reduced by using a 'guard
ring'. (See Figure 3.) Even without a guard ring the field within a parallel plate capacitor is uniform
except very close to the edges.
Let the area of the plates be A and their separation
d; let one plate have a charge +Q and the other -Q, and let the capacitance be C. Assume
the field between the plates to be uniform and that the charge density is also
uniform.
The charge density on the plates (
sA) is Q/A
and therefore the electric field intensity E between the plates is given by:
Electric field intensity (E) = s/e = QeA
But if V is the potential difference between
the plates we have: E = V/d = Q/
eA and therefore, since C =
Q/V
Capacitance (C) = eA/d
Therefore the capacitance
increases if the area of the plates is increased or their separation decreased. (See
Experiments/Capacitor parallel plate)
You can also see that the insertion of a
material with a high permittivity will increase the capacitance of a capacitor. An explanation
of this is given in the file on dielectrics.
(Please refer to the section on Electric fields for
an explanation of charge density and permittivity).
Example problems
1. Calculate the separation of the plates of an air filled capacitor of capacitance 25 nF if the plates have an area of 40 cm2. (Permittivity of free space (eo) = 8.85x10-12 Fm-1
Capacitance (C) = eoA/d = 25x10-9 = [8.85x10-12x40x10-4]/d
Therefore: d = 0.0014 mm
2. Calculate the capacitance of a pair of parallel plates of area 25 cm2 if they are separated by a piece of Perspex 0.1 mm thick. Take the relative permittivity of Perspex to be 3.5.
(Permittivity of free space (eo) = 8.85x10-12 Fm-1)
Capacitance = [8.85 x 10-12 x 3.5 x 25 x 10-4]/10-4 = 7.43 x 10-10 = 0.74 nF.
As explained in the file on capacitors an air filled parallel
plate capacitor with plates 1 mm apart and with a capacitance of 1 F would have plates each
of a tenth of a square kilometre!
Changing the plate separation of a parallel
plate capacitor
If we consider the formula for the parallel-plate capacitor we can
see what happens as we change the plate separation. There are two different cases to consider:
(a) where the capacitor remains connected to the source of electrical potential,
and
(b) where the capacitor is disconnected after the initial charge Q has been placed on
the plates.
(a) The potential V remains constant and therefore the charge on the
plates varies. This is because V = Q/C and C = eA/d. As the separation
of the plates is increased the charge on them decreases to maintain a constant value of V.
The electric field intensity between the plates therefore falls. The change in energy of the
capacitor is explained by the movement of charges in the wires as the capacitor partly
discharges to maintain the potential.
(b) If the supply is disconnected, however, then
it is the charge on the plates that remains constant and the potential difference between
them increases as the plates are separated. The electric field intensity remains constant in
this case. This can be explained by the fact that work has to be done on the plates to
separate them. There is an increase in the energy of the capacitor which can explained by
the addition of energy to moving the plates apart against their mutual
attraction.