Boolean algebra

In 1847 George Boole devised a simple method of analysing logic circuits, over a century before the first integrated circuit had been produced. Boolean algebra, as this branch of mathematics is called, operates with the following rules.

(Note: We will use A'' to represent A double overscore)

If A is the input to a circuit and the notation A' means NOT A then:
1. A + 0 = A
2. A+1 = 1
3. A.0 = 0
4. A.1 = A
5. A'' = A
6. A.A = A
7 A. A = 0
8 A+A = 1
9. A + A = A

Using this notation we can write down the outputs from the logic gates that we have considered.

OR output = A + B

AND output = A.B

NOT output = A

NAND output = [A.B]

NOR output = [A+B]

Now we can handle expressions in Boolean algebra in exactly the same way as normal algebra; however, the results will not mean the same as in normal algebra. For example:

A.(B + C) = A.B + A.C

but if we now give A, B and C values with A =1, B = 1, C = 0 then the final result using the rules above is:

1+0 = 1

We can apply these rules to the slightly more complex circuit in Figure 1.



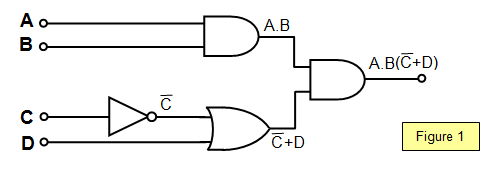
The final output is A.B(C+ D) and this can be multiplied out to give A.B.C + A.B.D
Using the values A = 1, B = 1, C = 0, D = 1 gives:

A.B.C + A.B.D = 1 + 1 = 1 and so the output of the circuit is 1