Errors and uncertainties in experiments

Any experiment will involve a series of measurements and each of these will be made to a certain degree of accuracy. For example the calculation of a velocity needs both a time and distance measurement. Therefore errors and inaccuracies in each measurement will give a final error in the result.
There are two basic types of error that may appear in the result:

Systematic errors

These are errors which are due to the apparatus and may result from either faulty apparatus, badly calibrated apparatus or a zero error.
The only way to eliminate systematic errors is to re-calibrate the apparatus or change it!

Random errors

These are errors that are due to experimenter - in others words us! The size of these errors depends on how well the experimenter can use the apparatus. The better experimenter you are the smaller will these errors be. The way to reduce these errors, apart from simply being careful, is to repeat the readings and take an average.

Precision and accuracy

It is important to understand the difference between the precision of a measurement and its accuracy. It is possible to measure something to a high degree of precision (for example a mass to a milligram using an electronic balance) but still to have an inaccurate answer because the instrument used had an offset zero error.

Quoting an answer

When you have made your set of readings you must be careful when you quote your result. You will probably use a calculator reading to eight digits to calculate and answer involving perhaps three of four quantities - do not use the eight digits - the accuracy of the final answer cannot be better than the accuracy of any of the single quantities.

A word of warning here: small quantities may only be ignored in comparison with large ones. For example in an answer such as 5.4000003 the 0.0000003 may be ignored in comparison to the 5.4 and the answer quoted as 5.4 but this is not the case in an answer such as 0.0000013 where the 0.0000003 is 23% of the answer. An Analogy: If you are sat on by an elephant it is not important whether or not the elephant has a fly on its back - you are still squashed flat. However to another fly the first fly is important!

Calculating an error

In this section we will imagine that we want to find the value of a quantity Q that involves the measurement of two other quantities a and b
There are two possibilities:
(i) Q is the sum or difference of a and b or (ii) Q is the product or quotient of a and b.

(i) Suppose that Q is the length of an object found by taking the reading of the position of its two end a and b from a ruler Q = a - b
Let the error in a be Δa and that in b be Δb. Then the error in Q is simply the error in a plus the error in b.
That is:

Then the value of Q should be written as:




(ii) Suppose that Q is the area of a rectangle with sides a and b so that Q = ab (Figure 4).


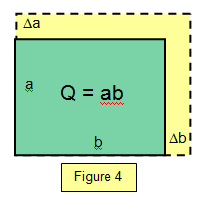
Let the error in a be Δa an that in b be Δb.
Therefore the maximum value of Q is :
Q + ΔQ = (a + Δa)(b + Δb) = aΔb +bΔa +ab +ΔaΔb
But we can ignore the quantity ΔaΔb since it will be very small compare with the other quantities in the equation and so:


and this is true whether or not Q is a product or a quotient.
If one of the quantities, say b, is raise to a power n (i.e. Q = abⁿ) the value of ΔQ becomes:


It is probably easier to understand these two equations if they are quoted as a fractional error. In other words:


or even easier as a percentage error:


Notice that pure numbers have no errors; this can be assumed for quantities such as p and e