Useful Mathematics for A level Physics

As you will realize, a knowledge of Mathematics will be very useful to you in parts of the Advanced Physics course.

The following suggests the basic requirements in mathematics for most Advanced level Physics syllabuses in school together with some extensions for more advanced Physics papers. It does not attempt to teach or explain the topics but simply lists them. You should consult your Mathematics or Physics teachers for further help. (Some of these topics may not be required for all syllabuses, however.)

Many of the topics include references to sections of the site where their use is demonstrated.

Students should be able to do the following:

Carry out calculations involving numbers in decimal form.

Make sensible evaluations of numerical expressions using reasonable approximations such as ? = 3.

Express small fractional changes as percentages and vice versa.

Use scientific notation and work out problems in this form.
For example:
1.6x10⁶ x 2x10⁵ = 3.2x10¹¹ [1.6x10⁶]/[2x10⁵] = 8 1.6x10⁶ + 2x10⁵ = 1.8x10⁶

Change the subject of an algebraic equation.
For example:
If A = BxC then C = A/B and so B = A/C

Solve algebraic equations of the form: ax² + bx + c = 0 using the formula
Roots of the equation = [-b ± (b² - 4ac)^1/2]/2a

For example: 2x² + 5x - 6 = 0
In this equation a = 2, b = 5 and c = - 6
The roots are: [-b + (b² - 4ac)^1/2]/2a and = [-b - (b² - 4ac)^1/2]/2a
So:
[- 5 + (25 + 48)^1/2]/4 = [-5 + (73)^1/2]/4 = [-5 + 8.54]/4 = 3.54/4 = 0.89 and
[-5 + (25 + 48)^1/2]/4 = [-5 - (73)^1/2]/4 = [-5 - 8.54]/4 = - 13.54/4 = - 3.38

Recognise the shape of various graphs (see Introduction, measurement and practical and the separate file in the Advanced section of the site named Graphs)

Recognise the equivalent forms of the logarithms of ab, a/b, xⁿ and e^kx

log (ab) = log a + log b
log (a/b) = log a - log b
log (xⁿ) = n log x
ln(e^kx)=kx

log implies a number to the base ten and was written as log₁₀.
ln implies a number to the base e and was written as log_e.

We now usually write log₁₀ as lg.
Logarithms to other bases (such as 2) would be written as log₂.

Change of Base from base 2 to base 10 – calculation of logs to the base 2 The logarithm log₂(x) can be calculated from the logarithms of x and 2 with respect to base 10 using the following formula:


For example: log₂(2000) = log₁₀(2000)/log₁₀(2) = 3.3010/0.3010 = 10.97 = 11

Use the binomial theorem to express quantities such as (1 + xn) for small x.

(1 + xⁿ) = 1 + nx (1 + x^-n) = 1 - nx

Calculate areas of triangles, circumferences and areas of circles, and volumes of rectangular blocks, cylinders and spheres.
Area of a circle = pr²
Circumference of a circle = 2pr (one dimension r)
Surface area of a sphere = 4pr² (two dimensions r to the power 2)
Volume of a sphere = 4/3pr³ (three dimensions r to the power 3)
Surface area of a cylinder = 2pr² + 2prL
Volume of a cylinder = pr²L
Surface area of rectangular block with sides a, b and c = 2ab + 4ac
Surface area of cube with sides a = 2a² + 4a² = 6a²
Volume of rectangular block with sides a, b and c = abc
Volume of cube with sides a = a³

Use and apply simple theorems such as Pythagoras'.

Use sine, cosines and tangents.
sin A = opposite side/hypotenuse
cos A = adjacent side/hypotenuse
tan A = opposite side/adjacent side

sin A = cos(90 - A)
cos A = sin(90 - A)

Recall and use the expansions of sin(A ± B) and cos(A ± B) as follows:
sin(A + B) = sinAcosB + cosAsinB
sin(A - B) = sinAcosB - cosAsinB
cos(A + B) = cosAcos B - sinAsin B
cos(A - B) = cosAcosB + sinAsinB

Recall the following identities:

sin²A + cos²A = 1
sin 2A = 2 sin A cos A
cos 2A = 1 - 2 sin² A

Recall that, when q tends to zero:
sinq tends to q ^c
cos q tends to 1 and
tan q tends to q^c
If q^c is the angle expressed in radians.

Find the resultant of two vectors and the components of a vector in two perpendicular directions.

Use graphical methods to display variables or find values for quantities, choosing suitable values for the axes and suitable scales

Understand the use of the area below a curve when this has a physical significance.
For example a curve of force against velocity. The area between the curve and the velocity axis is the impulse or momentum change of the object

Understand the use of the slope of a tangent to a curve to express rate of change.

Understand the meaning of the sum Sx.
For example:
For n = 1 to 10 Sxⁿ = x + x² + x³ + x⁴ ………………………. + x¹⁰

Be able to perform simple differentiation and integration:
d(xⁿ)/dx = nx^(n-1) For example: d(x³)/dx = 3x²

d(sin rx)/dx = r cos rx d(cos rx)/dx = - r sin rx

d(e^kx)/dx = ke^kx notice that when k = 1 we have d(e^x)/dx = e^x. This means that the gradient of the e^x curve at any point is equal to the value of e^x at that point.


Understand the relation between the derivative and the slope of the curve and also that between the integral and the area below a curve.

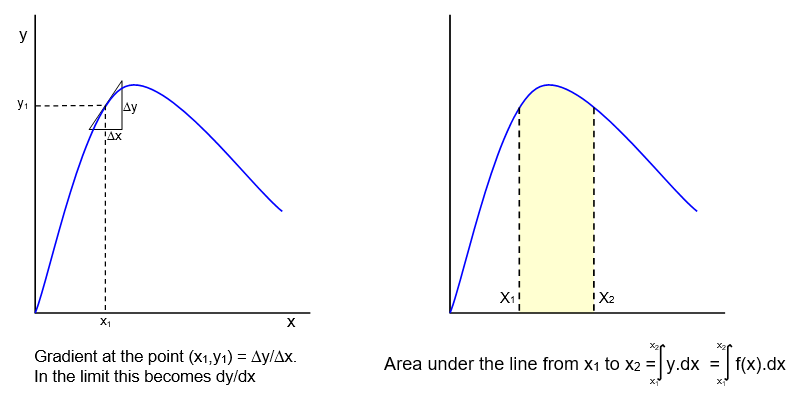
Be able to find the maxima and minima of a curve by differentiation.
For example a curve with an equation of: y = 5x² - 15
The maximum or minimum of the curve is given when dy/dx = 0.
So: dy/dx =10x - 15 = 0, the minimum occurs when x = +1.5
You can tell it is a minimum because d2y/dx² = +10 (positive)

However for a curve with an equation of: y = 15 +x - 5x²
The maximum or minimum of the curve is given when dy/dx = 0.
So: dy/dx =1 – 10x = 0, the maximum occurs when x = +0.1 (y = 15.05)
You can tell it is a maximum because d2y/dx² = -10 (negative)

Useful numbers: e = 2.7183; 1 radian = 57.3^o

Translate from degrees to radians and vice versa, where q radians = [2π/360]θ^o.