Cross product

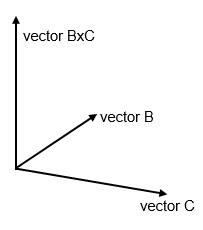
The vector cross product gives a vector which is perpendicular to both the vectors being multiplied. The resulting vector is defined by:

x = Ay * Bz - By * Az y = Az * Bx - Bz * Ax z = Ax * By - Bx * Ay

The cross product operation applies only to 3D vectors.
For instance in 2 dimensions it is not possible to find another vector which is mutually perpendicular to 2 arbitrary vectors. The cross product can be used to calculate the Normal to a surface.

A x B = - B x A

Vector cross multiplication is not commutative, changing the order reverses the direction of the resulting vector.

If A,B and C are vectors and x is cross multiplication, then,
A x (B + C) = (A x B) + (A x C)

The cross product (BxC) is always at right angles to the two vectors B and C and takes the direction of a right handed screw.

Dot product

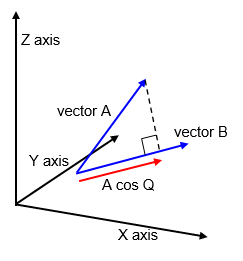
This is essentially the magnitude of the projection of one vector onto another vector multiplied by the value of the second vector. It is the component of the vector along that line times the value of the second vector.

|A|.|B| =|A||B| cos Q where Q is the angle between the two vectors.
The result of the dot product is a scalar and not a vector.

It is defined as Ax*Bx + Ay*By + Az*Bz

Where Ax etc. are the components of the two vectors in the x,y and z directions.