
If a car corners on a flat road then the frictional forces between the car tyres
and the road provide the centripetal force to make it take the curve. It is important to understand
that there is not an additional force (mv2/r) - the frictional force is equal to the centripetal
force - in actual fact it is the centripetal force.
The
design of the car determines the maximum speed at which it can travel round a certain curve
without tipping over. As you would expect the car with the lowest centre of gravity and the widest
track will be able to corner the quickest. This is shown in the proof below where this maximum
speed is found.
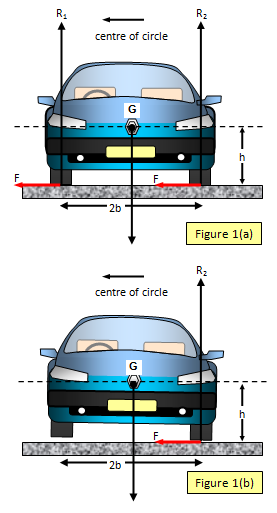
Let the height of the centre of gravity above the ground be h, the track
width 2b, the speed of the car v, the radius of the curve r, and the mass of the car m. The
reactions of the road of the inner and outer pairs of wheels are R1 and R2
respectively and the frictional force between the tyres and the road is F.
(See Figure
1(a)).
When the car is just about to fail to take the curve the inner wheels lift off the
ground and so R1 will become zero. (See Figure 1(b)). The car will then tend to topple
over outwards away from the centre of the corner.
Resolving vertically: R2 =
mg
Taking moments about the centre of gravity :
R2b = Fh and so F =
R2b/h = mgb/h
But since F = mv2/r we have mv2/r =
mgb/h
and so the maximum speed at which the car can take the curve is given by
:
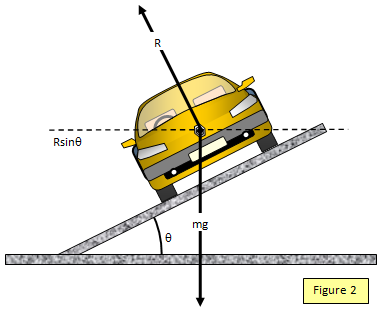
In this case it is the component of the weight of the car
towards the centre of the curve that provides the centripetal force. Notice that there is no additional
force mv2/r - the component of weight is the centripetal force. (See Figure 2)
If the
track is banked at and angle q to the horizontal then:
Resolving horizontally and
vertically:
Rsinq = mv2/r and Rcosq =
mg
where v is the maximum speed that the car can take the corner.