
As you know according to Newton's First law a
body remains at rest or travels in a straight line unless an unbalanced force acts on it. So to make
a body travel in a curve a force must act to pull the body away from its straight line. This curved
path could be a parabola, as in the case of a projectile moving in a gravitational field, a hyperbola,
as for an alpha particle near a nucleus, an ellipse, planets in motion round the Sun or a circle, as
in a stone whirled round your head on a string.
In a circle the radius is always at right
angles to the motion and since the string is the radius of the circle the force that acts on the stone
must be along the string - at right angles to the path of the stone.
Examples of "everyday"
circular motion are given below together with the force that makes the paths circular.
| Example | Force |
| Centrifuge | reaction at walls |
| Aircraft banking | component of lift on the wings |
| Electron orbits | electrostatic force |
| Car cornering | friction between road and tyres |
| Planetary orbits (almost!) | gravitation |
| Car cornering on banked track | component of gravity |
| Rotating liquid | gravity |
| Car tyres rotating | tension in the tyre |
| A CD | tension in the CD |
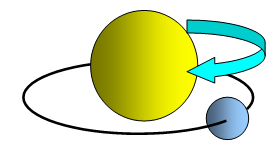
The force that pulls an object out of a straight line path into a circular orbit is called the centripetal force. (The word means centre seeking). It is the force on the orbiting object.
Thinking about the stone being whirled round on the end of a string. From Newton's Third Law states we know that if a force acts on the stone then there must be an equal and opposite force acting on another body - this will be a force on the hand holding the string and this force is known as the centrifugal force (the word means fleeing from the centre). If you like to put it this way the centrifugal force is the reaction of the centripetal force on the pivot. As far as the orbingt object (in this case the stone) is concerned the centrifugal force is a fictitious force – it does NOT act on the stone.

If you remove the centripetal force, in the example of the stone and string by cutting the
string, the stone will move off along a straight line in the direction it was moving at the instant the
string was cut along the tangent to the circle (ignoring gravity for a moment) and not along a
radius.
The photograph shows a sparkler being spun in a vertical circle. It celarly shows that the small particles of burning metal move in straight lines when the become detatched from the sparkler.
Angular displacement is expressed in radians. A radian is defined as the angle subtended at the centre of
the circle by an arc of length equal to the radius of that circle. In one complete circle there are 2π
radians and so one radian equals just over 57o.
When an object is travelling in a circle it has an instantaneous linear
velocity but it also has an angular velocity (w). This is defined as the
rate of change of angle with time and is usually expressed in radians per
second.
For a rotating body that is rigid such as a CD or a wheel the angular
velocity is the same at all points on the body while the linear gets greater as the distance from the
centre gets larger. However if the body is not rigid like soup in a bowl that is being spun round the
angular velocity changes. A fun experiment to demonstrate the forces in rotating objects and to
simulate what happens to a spinning car tyre is to rotate a jelly on a turntable and see when it
begins to break apart.
If we take T to be the time for one complete rotation - called the
period of the motion then
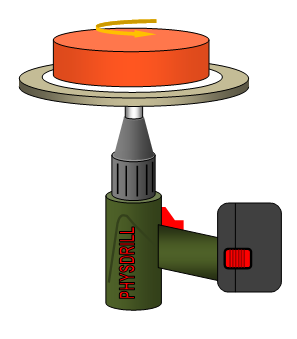
A very good way to simulate the break up of car tyres is to make a jelly and put it on a rotating table. As the rate of rotation of the table is increased so the jelly spreads out and flattens. The forces within the jelly keep it together but a point will be reached where these forces are no longer great enough, it can no longer stay in one piece and flies apart, just like car tyres on a motorway.