
If you drop a power ball onto a hard piece of ground from a height of 1 m it will bounce up to around 80 cm – some of the original gravitational potential energy is lost in the collision.
Now imagine that no energy is lost – the ball will rebound to exactly the same height from which it was dropped – in other words 1m.
Take a second ball and drop the two together with the smaller ball resting on top of the larger one. The large ball hits the ground first, deforms slightly and then begins to move upwards – meeting the smallest ball whose centre of mass is still coming down.
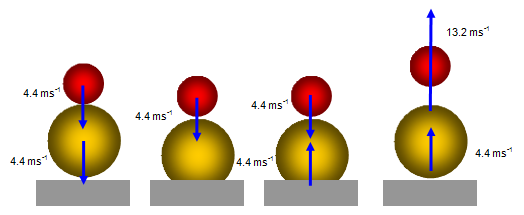
The diagrams show what happens. If they have been dropped from 1m above the Earth’s surface both balls are travelling at 4.4 ms-1 when they collide – the large one moving upwards and the small one moving downwards. What happens now is similar to throwing a tennis ball at a train! When the train is stationary the ball rebounds with roughly the same speed that it had originally (say 12 ms-1).
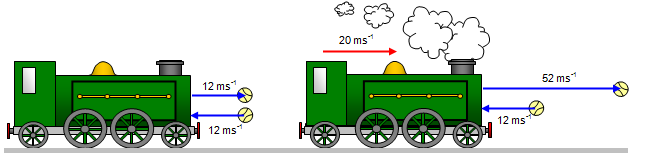
However if the train is moving towards the thrower at say 20 ms-1 the approach speed of the ball and train is 12+20 = 32 ms-1. This means that the speed rebound of the ball relative to the train is also 32 ms-1 but in the opposite direction. Relative to the GROUND the ball is now moving at 32+20 = 52 ms-1! Assume that the impact of the ball has no effect on the speed of the train.
Going back to the balls the approach speed of the two balls is 8.8 ms-1 so the rebound speed of the small ball RELATIVE TO THE LARGE BALL is 8.8 ms-1 and so the speed of the small ball RELATIVE TO THE GROUND is 8.8+4.4 = 13.2 ms-1 and it will reach a height of 8.9 m.
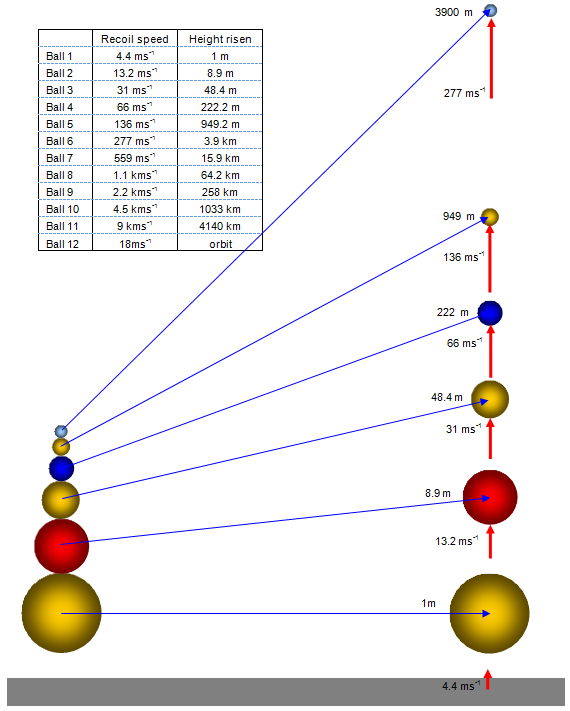
Imagine now that you have a set of six balls, each one being much smaller than the last with ball 1 being the biggest (heaviest). If you carefully stacked the balls one on top of the other and dropped the pile vertically onto the hard ground some amazing things happen. Each ball acts on the one above it and the result is an extension of the effect with only two balls.

The results are shown in the diagram (not to scale) and in the table. Ball 6 will reach just over 3900 m – nearly half the height of Mount Everest and its speed of ‘rebound’ will be almost 280 ms-1. If we could drop a stack of twelve balls ball 12 would reach a speed of over 18 kms-1, greater than the escape velocity of the Earth and travel off into space!
Remember that all this assumes no loss of energy on impact, each successive ball must be much less massive than the one below it and air resistance must be ignored.