
Although you would not play snooker using a protractor and a calculator to work out your shots the study of momentum is crucial in what actually happens!
We will first consider the more simple case where
the two balls collide along a line joining their centres. We have to assume that the two balls
are not only exactly the same mass (m) but that the collision between them is perfectly
elastic - remember that this means that no kinetic energy is lost in a collision. First think of
just one stationary red being hit head on by the white.

After the collision the white ball stops dead and
the red ball moves off with the velocity that the white ball had before the collision. (This is
only exactly true if the two balls are sliding and not rolling!)
We can prove this as
follows:
Momentum before collision = momentum after collision muA =
mvA + mvB
But because the collision is elastic kinetic energy
is also conserved and so:
½ muA2 = ½
mvA2 + ½ mvB2
The masses can be
cancelled giving:-
uA = vA +vB and
uA2 = vA2 + vB2
Using a little algebra to combine these two equations will show you that:
In fact it can be proved that when two equal masses collide elastically their velocities are swapped over. If mass A had a velocity u before collision and mass B a velocity v, then after collision A moves with velocity v and B with velocity u.
Both balls move off at an angle to the original direction of the white.
The interesting thing is that the angle between the red and the white balls is exactly 90o, in
theory. The big problem here is spin - if you put some "side" (spin) on the white the angle
will be different.
Assuming no spin and that the collision is elastic:
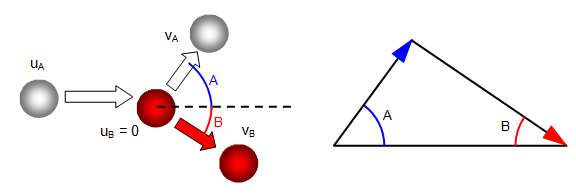
The vector triangle for velocity must be right angled (Pythagoras). Remember that velocity and therefore momentum is a vector but kinetic energy is a scalar and so we can simply add the kinetic energies of the balls after impact without allowing for their different directions of motion.
