Vacuum filled box!

Question: How does a hollow object "filled" by a vacuum act when a hole is created in one side.
For instance, assume that we have a hollow cube, and there is a vacuum inside it at a very high pressure. If one of the sides were pierced, what would be the overall force on the box? Would it move in any direction?

Answer:

Basically the ideas show that the box will accelerate in the direction of the hole while the jet of gas is moving across the box. When the jet strikes the far wall the acceleration will cease but there will still be a velocity to the left (the side with the hole in it).

The motion of an evacuated box in a region of high pressure when a hole is made in one face

Force on any face of the box = Pressure x Area of face

Therefore if the face has a hole in it the pressure on that face is decreased and so the force on that face is decreased.

I have assumed that both the hole and the jet can have an area of anything from 0 up to the area of the whole face.


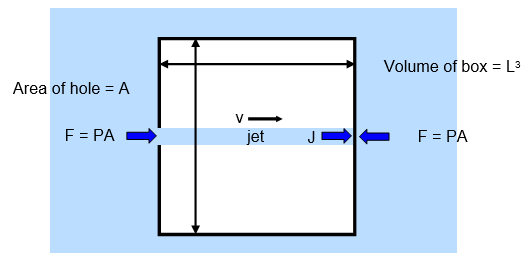
For simplicity lets assume that the environment is a zero gravity one.

Density of gas = r   Initial pressure of gas outside box = P

Let a equal the momentum produced per second as fluid enters the jet
= momentum destroyed per second as the jet strikes the opposite face of the box.

Applying Newton's Second Law to the production of the jet. F = a

Applying Newton's Second Law to the destruction of the jet J = a and so J = F

Therefore there is no resultant force on the box while the jet is striking the opposite face of the box.

However before the jet reaches the opposite face of the box there is a resultant force F = PA on the box to the left and this force is proportional to A, the cross sectional area of the jet.

Calculation of v (the velocity of the box)

a = Av x (density of fluid) x v = Arv² = PA

Where r is the density of the fluid.

F = Arv² and this gives v = [Density/Pressure]^1/2 = [r/P] ^1/2

Therefore v is independent on the cross sectional area of the jet and therefore the size of the hole.

Calculation of time for jet to reach the other side of the box

This is L/v = L[r/P] ^1/2

Graph of resultant force R to the left on the box before jet strikes the opposite face

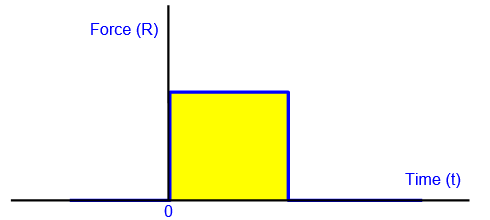
Hole appears at t = 0.

Momentum change given to the box = Impulse I given to the box = area under the line = PAL[r/P] ^1/2 = AL[rP]^1/2

Graph of impulse (I) against A

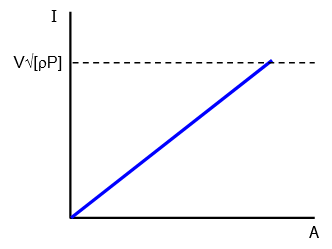
I = AL[rP] ^1/2

I_max = L²L[rP] ^1/2 = L³[rP] ^1/2 = V[rP] ^1/2