The shopping bag or rescue helicopter
A plastic shopping bag can carry
a lot of heavy shopping but if you try to lift it up quickly the handles break - why is
this?
This is because the bag has to do two things when you lift it quickly.
First support the shopping (mg) and secondly accelerate it upwards (ma).
As
you know acceleration needs a force and so this extra force must be supplied through the
handles. If they are not strong enough they snap. The greater the mass of the shopping the
greater its inertia and the more force is needed to accelerate it.
Force in the handles = mg + ma = weight + accelerating force
Moral - always lift shopping
slowly!
The same problem
occurs when a rescue helicopter lifts a stretcher off a mountainside – the combined weight of
the patient and the stretcher plus the accelerating force must be less than the breaking force
in the lifting cable.
Example problem
A stretcher and patient have a combined weight of 800 N. What is maximum acceleration possible using a cable with a breaking force of 2000 N allowing a safety factor of two?
Safety factor means that the greatest force in the cable must be 1000N.
Force “available” for acceleration = 1000 - 800 = 200 N
Acceleration = F/m = 200/80 = 2.5 ms-2.
The same thing could happen in a lift
that accelerated upwards quickly - people standing inside the lift holding their shopping could
find the handles of their plastic shopping bags snapping!
As you get older it is more
important than ever to "warm up" properly before running. Your muscles get less flexible with
age and the sudden forces produced in sprinting can cause them to tear in extreme cases.
Example problems
1. Two masses over a pulley
A rope with zero mass passes over a frictionless pulley. (I know that this is impossible but it makes the problem easier!) To one end of the rope is tied a mass of 2.4 kg and to the other a mass of 4.6 kg. Calculate their acceleration.
Resultant force in the rope = (4.6 - 2.4)g N = 2.2g N = 21.56 N. This force accelerates a total mass of 7 kg.
Therefore using F = ma
Acceleration = F/m = 21.56/7 = 3.08 ms
-2 = 3.1 ms
-2
2. Car and caravan
A car of mass 1500 kg tows a caravan with a mass of 1000 kg along a level road. Assuming that frictional drag has been allowed for and that the car accelerates at 3.5 ms
-2 pulling the caravan with it calculate:
(a) the force of the car on the caravan
(b) the force of the caravan on the car
Since there is no relative motion between the car and the caravan the forces mentioned in (a) and (b) are the same size but are opposite in direction.
Force = 1000x3.5 = 3500 N
(notice that it is the mass of the caravan and not the car that is used here).
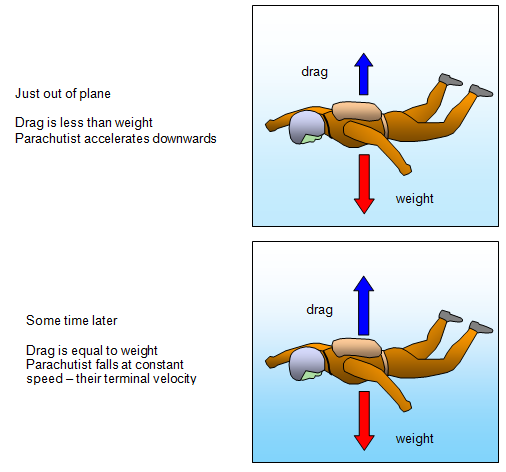
Free fall parachutist
A sky diver
leaves a plane and starts to fall towards the ground. Initially their weight exceeds the drag on
them due to the air and so they accelerate downwards. As the speed increases so does the
drag until drag = weight. Then the parachutist falls at a constant terminal
velocity.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB