
A very good example of Newton's
Laws is shown by the following situation.
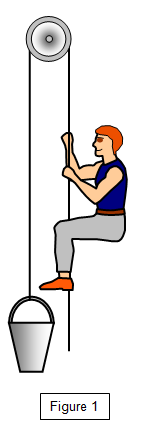
A bucket of bricks of mass 120 kg is tied to one
end of a rope which passes over a frictionless pulley so that it hangs vertically downwards. A
man of mass 80 kg hangs onto the other end of the rope.
Calculate:
(a) the tension in the
rope holding the man
(b) the tension in the rope holding the bucket
(c) the
acceleration of the man
(d) the acceleration of the bucket of bricks
(e) the tensions in
the two sections of the rope if it is held stationary on the pulley.
Taking g = 10 ms-
2
Let the tension in the rope be T and the acceleration of the man and bucket of
bricks be a.
(a) Consider the forces on the man
T – 800 = 80a
Now
consider the force on the bucket
1200 – T = 120 a
Combining these two
equations gives:
a = 2 ms-2 T = 960 N
(b) Since T is the tension
throughout the rope the tension in the rope holding the bucket is also 960 N
(c)
and (d) a = 2 ms-2
(e) If the rope is held stationary it effectively becomes
two sections of rope, with a different tension in each.
800 N (man) 1200 N (bucket
and bricks)