
Can a window cleaner (mass m) standing on the gantry (mass M, M>m) go up a
building using only a rope over a pulley although the total weight on the gantry is more than
his own weight?
This is another problem where we will have to use some
mathematics. First consider the case when he is not standing on the gantry but simply
hanging on the rope. The net force on the man is Mg - mg so he rises, his acceleration being
[(M-m)g/(M+m)]. For example if the man and the gantry are both the same mass everything
stays still but if the gantry is twice as heavy as the man then he will ascend at g/3. Of course
if he is heavier than the gantry he will descend.
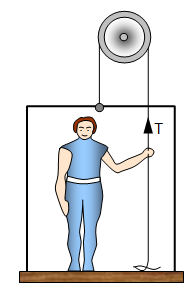
Anyway, he now stands on the gantry.
The forces on the man are
now given by the equation: T + R - mg = ma
and those on the gantry by : T - R -
Mg = Ma
Once again if the window cleaner is lighter than the gantry he will be
pulled up until he jams his fingers in the pulley at the top!
To show this, take the
second equation from the first giving:-
2R = ma+mg - Mg - Ma = g(m-M) +a(m-M) and so
2R = g(m-M) +a(m-M)
Now if m << M the right hand side of the equation will
be negative and the reaction will also be negative - in other words the gantry will fall away
from the cleaner. So the answer to the original question is no!
However this time if
he is heavier than the gantry he can make a controlled ascent.
Clearly the window cleaner will be jerked off his feet if the gantry is heavier that he is. If he is heavier than the gantry whether he moves up or down will depend on his pull on the rope and hence the reaction transmitted by his feet to the floor of the gantry.