Newton's Second Law
This law is all about the situation when there
is a resultant force and therefore there is also an acceleration.
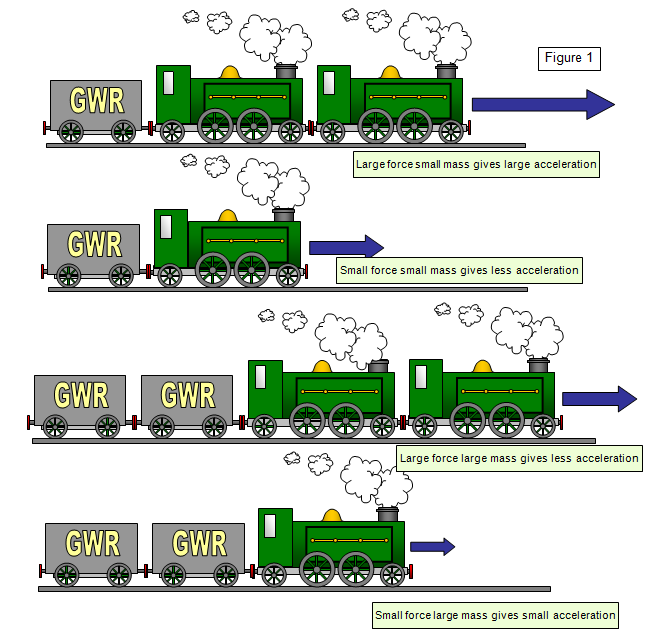
You need a force to change the motion of a
body. The bigger the net force the greater the acceleration. (remember that force is a vector
and the direction of the forces acting on a body need to be considered). Aristotle thought that
the force was in the same direction as the motion (i.e. the velocity). This is not true - the
force is in the same direction as the acceleration if you don't follow this think of a basket ball
being thrown into a net. the ball follows a curving path in the air but the force - and therefore
the acceleration is always in one direction - vertically downwards.
You can
investigate the law practically by using a linear air track and measuring the acceleration of
the truck for a variety of accelerating forces and truck masses. The linear air track is the best
equipment to use since the force of friction is very low.
It is also important to remember
that the mass being accelerated is the total mass of the truck plus the mass of the
accelerating weight although this is not significant if the truck is very heavy in comparison.
The results can be analysed by plotting two graphs - one of the acceleration against the
accelerating force and the other of acceleration against the inverse of the mass of the truck
(1/m)
This should show you that the :
(a) acceleration is directly proportional to
the accelerating force and
(b) acceleration is inversely proportional to mass of the body
being accelerated
Combining these two results gives
Force = mass x acceleration
The units for force are Newtons (N), mass
are kg and acceleration ms
-2.
This law also gives us a good definition of the
Newton as a unit of force.
One Newton is the force that will give a mass of 1 kg an acceleration of 1 ms-2
Example problem
Line of blocks
A line of five blocks all with a mass M rest on a smooth horizontal table. They are accelerated by a force F pushing on block A. What is the :-
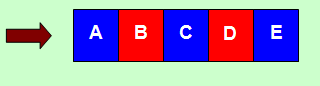
(a) acceleration of block C?
(b) force of block B on block C?
(c) force of block C on block D?
(d) force of block E on block D?
(a) Using F = ma we have
Acceleration = F/5M for the whole set of blocks, however since the blocks do not separate this must also be the acceleration of each block.
(b) block B pushes three blocks in front of it so the force of B on C is given by Force = 3Ma = 3F/5
(c) block C pushes two blocks in front of it so the force of C on D is given by Force = 2Ma = 2F/5
(d) the force of E on D is equal but opposite to the force of D on E - in other words F/5
Although we may think of the
second law as "Force equals Mass times Acceleration" Newton actually stated his famous
law as follows:-
The rate of change of momentum of a body is directly proportional to the applied force and in the direction of that force.
Expressed mathematically Newton's Second Law is:
Force = d(mv)/dt where mv is the
momentum of the object.
Now if mass is constant then F
= d(mv)dt = mdv/dt = ma - consistent with the simple statement of the law.
Newton’s second law: Force = d(mv)/dt = ma
Example problems
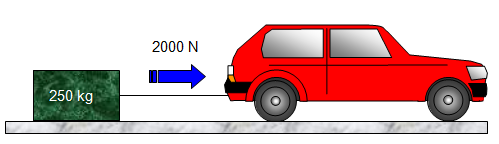
1. Simple use of F = ma
A 250 kg box is pulled along a smooth road (no frictional drag) using a force of 2000 N. What is the acceleration of the block?
Therefore using F = ma Acceleration = F/m = 2000/250 = 8 ms
-2.
Note that mass is measured in kg - do not convert the mass to a weight!
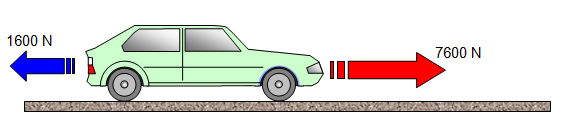
 2. Car with drag
2. Car with drag
This example shows the need to find the resultant force before using F = ma.
In other words
Resultant force = Thrust - Drag.
A car of mass 1200 kg has an engine with a thrust of 7600 N. It accelerates along a road where the frictional forces acting against its motion are 1600 N.
Calculate the acceleration.
Resultant force = 7600 - 1600 = 6 000N Therefore using F = ma
Acceleration = 6 000/1200 = 5 ms
-2.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB