HOME > AGE 16-19 > MECHANICS > DYNAMICS > ROCKETS

Rockets

The propulsion systems of rockets depend on the taws of momentum conservation. For a solid or liquid fuel rocket, the greater the velocity of the exhaust gases the greater is their momentum and hence the greater the momentum of the rocket.

The table below gives the exhaust gas velocity for a variety of different fuels.

Fuel	Exhaust gas velocity (ms^-1
Hydrogen and oxygen	5800
Acetylene and oxygen	5500
Petrol and oxygen	5000
Kerosene and oxygen	5000
Alcohol and oxygen	4850
Smokeless gunpowder	3500
Gunpowder	2600

Alternative propulsion systems have been proposed and these include nuclear engines, ion drives and even explosive drives!

The calculation of the velocity of a rocket some time after its launch is a difficult problem, since the mass of the rocket is constantly changing and therefore even with a constant thrust the acceleration will not be constant. The velocity of the rocket when its mass is M can be shown to be:

Velocity of rocket (v) = u - w ln(M/M_o)

where u and M_o are the initial velocity and mass of the rocket and w is the velocity of the exhaust gases relative to the rocket.

Example problem
A rocket of mass 1000 kg accelerates from rest. If the velocity of the exhaust gases is 5000 ms^-1 calculate the velocity of the rocket when 100 kg of fuel have been used.
v = 0 – 5000 ln(900/1000) = 527 ms^-1

Student investigation

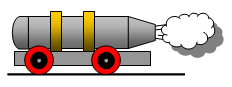Astronauts and fighter-pilots have been trained on rocket-powered trolleys to test their ability to withstand high accelerations. In your foundation courses you may well have seen a carbon dioxide powered version of the rocket trolley, such as the one shown in the diagram.

It consists of a small carbon dioxide cylinder such as those used in a soda syphon, mounted on a small trolley. The trolley is propelled by releasing the gas from the cylinder by piercing the end with a needle.

Using such a trolley, devise and carry out experiments to measure the following
(a) the average velocity of the trolley
(b) the maximum velocity of the trolley
(c) the average force exerted by the gas
(d) the average exhaust gas velocity.

A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB

Top of page