The geostationary satellite
This type of satellite gets its name from the fact
that it is launched into an orbit such that it has a period of exactly one day and so remains
constantly over one point on the Earth's surface. To be geostationary it must have an orbit that
lies in the plane of the equator. Photographs taken from a fixed camera aboard such a satellite
would always show the same view of the Earth's Surface.
Using the relations:
F = GMm/r
2 = mv
2/r and that v = 2
pr/T we have 4
p2/T
2 = GM/r
3
and so r = (GMT
2/4
p2)
1/3 = (g
oR
2T
2/4
p2)
1/3
Radius of orbit for a geostationary satellite = (goR2T2/ 4p2)1/3
F = GMm/r
2 = mv
2/r and that v = 2
pr/T
we have 4
p2/T
2 = GM/r
3 and so r = (GMT
2/4
p2)
1/3 = (g
oR
2T
2/4
p2)
1/3For the Earth
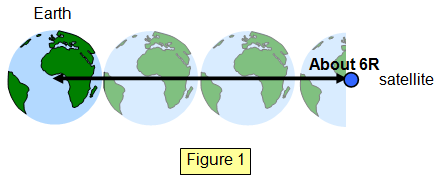
all synchronous satellites are in an orbit 42000 km from the Earth's centre - a potential problem for
cosmic junk!
Example problem
Calculate the orbit radius for a synchronous satellite orbiting Mars. Surface gravity for Mars = 3.80 ms-2, radius of Mars = 3.4x106 m, one Martian "day" = 8.86x104 s.
Radius of orbit = (goR2T2/4p2)1/3 = (3.80x(3.4x106)2x(8.86x104)2/4p2)1/3 = 2.06x107 m = 20 600 km
Summary of the properties of a geostationary satellite (for the
Earth):
(a) they have an orbit which lies in the same plane as the equator of the Earth
(b)
the period of the satellite is one Earth day
(c) they have the same angular velocity as the
Earth
(d) the move around their orbit in the same direction as the rotation of the Earth
(e)
they remain above a fixed point on the Earth's surface
(Some of these points overlap
others)
Example problems
The Moon has an orbit radius of 3.8x108 m and a period of 27.3 days. Use this information to calculate the radius (RS) of the orbit of a geostationary satellite.
Use: T2/R3 = constant Period of satellite = 1 day therefore:
RS3 = [3.8x108]3/27.32 = 7.36x1022 and so:
RS = 4.19x107 m = 41 900 km
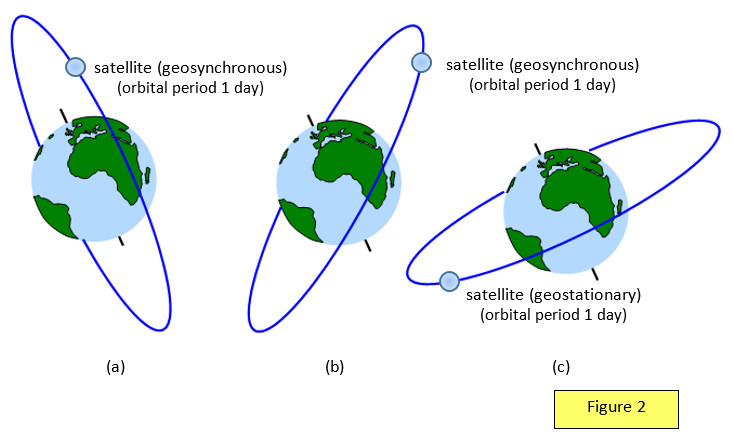
A satellite that orbits the Earth so
that it passes over a fixed point on the Earth's surface at the same time each day is called a
geosynchronous satellite. Such a satellite need not have its orbit in the plane of the equator but
the orbit radius will be the same as that for a geostationary satellite.
All the diagrams in Figure 2 ((a), (b) and (c)) show geosynchronous satellites, but only (c), in an equatorial orbit, is a geostationary satellite.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB