The measurement of the universal constant of gravitation (G)

During the eighteenth century many ingenious methods were devised to measure G. Accurate results were extremely difficult to obtain, however, because of its very small value.

The first experiment was performed in 1740 by Bouguer, who measured the deflection of a plumb line from the vertical due to the attraction between the plumb bob and a mountain (Chimborazo in the Andes) and from this calculated the mass of the Earth and hence G.
Other experimenters were Airy (1854), who measured the change in the acceleration of gravity down a mine, and von Jolly (1878) and Poynting (1891) who used the deflection of a large balance. All these experiments led to values of G but they are now really only of historical interest.

The basis of the modern method for G was an experiment carried out in 1789 on Clapham Common by Henry Cavendish. He used a large torsion balance and measured the twist in the torsion wire due to the attraction between two large fixed lead spheres 30 cm in diameter and two small lead spheres 5 cm in diameter attached to a beam at the base of the torsion wire. This experiment was greatly improved in 1895 by Boys, and it is this method that will be described fully.

Boys' method for the determination of G

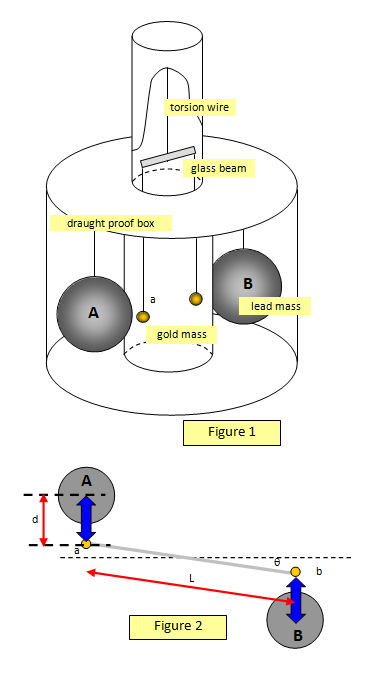
The apparatus is shown diagrammatically in Figure 1. Two gold spheres (a and b) 5 mm in diameter and with a mass of 3 g were suspended at different heights from either end of a 2.3 cm bar. This bar was hung from a quartz fibre torsion wire, 1 m long and with a diameter of 0.000 O5 cm! This arrangement was placed in a draught proof box, and outside this were hung two large lead spheres (A and B), 115 mm in diameter and each with a man of 7 kg. These were then enclosed in an outer box. The spheres were mounted at different levels to minimise cross-attractive forces between a and B and between b and A. The whole apparatus had to be mounted on a stable base to prevent vibrations.


The plan view (Figure 2) shows the forces acting on the spheres. The forces between the small masses and the large masses cause the beam to twist through an angle θ as shown in the diagram.

Let the separation of the centres of A and a and B and b be d, and let the beam have a length
Then torque on the beam = GmML/d²= cθ
where c is the torque in the torsion wire per radian twist. Therefore:
G = cθd²/mML


The torsional constant was determined by allowing the beam to oscillate and measuring the period of oscillation (T). Using the equation

T = 2π [I/c]^1/2
c can be found if the moment of inertia (I) of the beam and the small spheres is known.

The period was found to be about 2 minutes compared with the 7 to 8 minutes that Cavendish had found with his apparatus, which had a 1.8 m long beam!

Heyl repeated the experiment in 1942 using a lamp and scale 7 m away as a pointer and claimed an accuracy of 0.75 minutes of arc, giving G to better than one part in 10 000. Heyl and Brown also devised a method where a large mass was brought up briefly to a small mass suspended on a beam and the period of the resulting oscillations measured.

Up to the time of writing no substance has been discovered that shows a screening effect for the gravitational force so no anti-gravity machines have been devised! It is also assumed that this force travels with the speed of light. Efforts to detect gravity waves (see below) or quanta of gravitational force (gravitons) have also been unsuccessful.