
The gravitational potential (VG)at a point in a field can be defined in
two equivalent ways:
(a) the work done in bringing unit mass (i.e. 1 kg) from infinity
to that point or
(b) the potential energy of a unit mass placed at that point in the field
with the zero at infinity.
Since the gravitational field is attractive and the zero is at
infinity the gravitational potential is negative.
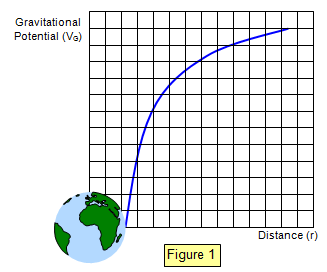
The variation of potential against
distance r for a mass M is shown in Figure 1 and is given by the equation:
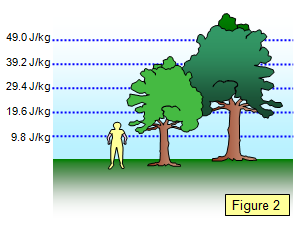
Close to the surface of the Earth the gravitational field is effectively constant and equal to 9.8 Nkg-1. The gravitational potential therefore increases steadily as the distance above the ground increases (see Figure 2).
The gravitational potential energy of a mass m is the energy required to bring the mass m from infinity to a point on the field. It can be calculated by simply multiplying the gravitational potential at the point by the mass m. It is important not to confuse this with gravitational potential, the gravitational potential energy refers to a mass m and so the gravitational energy at a point in the field distance r from the centre of the mass that is producing the field is:
Using our
ideas about potential energy we can sketch the variation of potential between the Earth
and the Moon and so predict the effects on a spacecraft on a journey between the two
bodies.
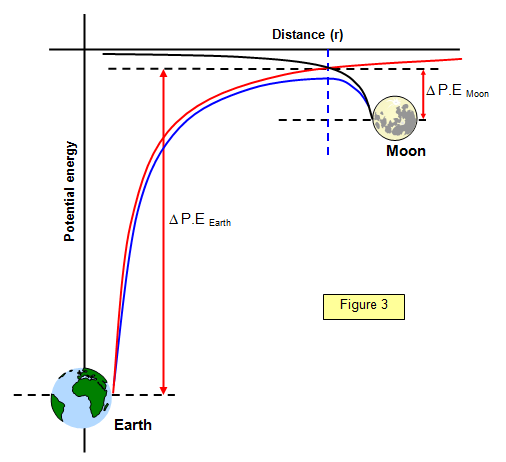
On the accompanying graph (Figure 3) the red line represents the
potential due to the Earth, the black line the potential due to the Moon and the blue line the
combined potential. You can see that there is a peak. To make the journey from one
direction or the other you must cross the peak. It therefore takes a lot more energy to
reach this if you start from the Earth than if you start from the
Moon.