Gravitation

Although Kepler had proposed laws of planetary motion they did not explain WHY planets orbited the Sun. It was left to Sir Isaac Newton (1674-1727) to suggest the reason and to propose the idea of gravitational fields. He realised that the force that holds the moon in orbit around the earth was the same as that which pulls an apple to the earth when it falls from a tree.

Newton and Kepler's Laws

In 1666, when he was still only twenty four years old, Isaac Newton, attempting to find a law of force that would be consistent with Kepler's third law proposed his universal law of gravitation. He considered a planet (mass m) moving in a circular orbit (radius r) at angular velocity ω round the Sun (mass M)

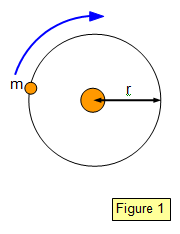
Force on a planet = F = mω²r = mr(2π/T) ² = 4π²mr/T²

Newton took the crucial step and assumed an inverse square law of force between the bodies, that is:

F = km/r²

where k is a constant. This assumption formed the basis of his law of universal gravitation.
Using the centripetal force formula we have:

F = mv²/r = km/r² = 4π²mr/T² and so
T² = 4π²r³/k and therefore T²/r³ is constant (and equal to 4π²/k).

This shows that the inverse square law of force is consistent with Kepler's third law - theory and observational results had agreed.

Newton's law of gravitation

We call Newton's constant (k) the universal constant of gravitation and it is now written as G. The value of G has been found to be 6.67x10^-11 Nm²kg^-2

Newton's Law of universal gravitation then becomes:



r is the distance between the centres of the two masses (Figure 2)

Mass of the Sun

The mass of the Sun (M) can now be calculated.
Gravitational force on a planet (mass m) = GMm/r² = Centripetal force = mv²/r
But orbit period (T) = 2rπ/v and so