
Objects moving through air are slowed down
due to air resistance, sometimes called drag. This air
resistance affects a spacecraft when it re-enters the Earth's atmosphere but also the path of
a projectile such as a bullet or a ball. When air resistance is taken into account the trajectory
of a projectile is changed. The resistance is often taken as being proportional to either the
velocity of the object or the square of the velocity of the object.
The medieval
scientists believed that a projectile went upwards at an angle along a straight path, then went
through a short curved section before falling vertically back to the ground
again.
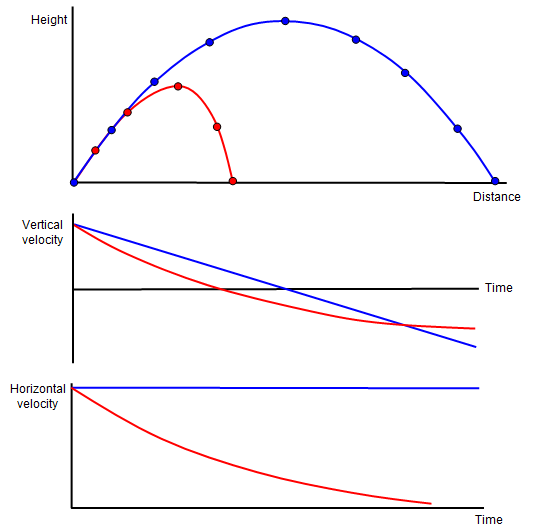
Both the range of a projectile and the maximum height that it reaches are
affected by air resistance. The mathematics of the motion is quite complicated (especially if
you consider the change in the shape and/or surface of a projectile and the variation of the
density of the air with height) but the following diagrams try to simplify things by showing
generally how air resistance affects both the trajectory and the velocity of a
projectile.
The blue lines show the projectile with no air resistance and the red lines
show what happens when air resistance is taken into account. The maximum height, the
range and the velocity of the projectile are all reduced.