Object projected horizontally
This page looks at an object projected
horizontally from a cliff with a velocity u. The problem is to find out where this object will be after
a time t and how fast it will be travelling and in what direction. (See Figure 1)
The
important thing to remember is that you can consider the motion in two parts :-
(a) motion
in the horizontal direction - this is uniform velocity since no forces act in this direction
(b)
motion in the vertical direction - this is uniformly accelerated motion due to the gravitational pull
of the Earth, the vertical acceleration being the strength of the Earth's field (g = 9.8 ms-
2). Remember that this always acts vertically downwards.
We will ignore air resistance
for the time being.

Consider
the horizontal motion:
The velocity after time t = v
x = u since there is no horizontal
acceleration
The horizontal distance travelled (s) = horizontal velocity (vx) x time (t) = ut (1)
Now
consider the vertical motion:
The initial vertical velocity (u
y) = 0 and so the vertical velocity
after a time t is given by
V
y = u
y + gt
Therefore v
y =
gt
The vertical distance travelled (h) = uyt + ½(gt2) = ½(gt2)
since uy = 0 (2)
Using Pythogoras' theorem the velocity (v) after a
time t can be found from the equation:
Velocity(v) after a time t = (vx2 + vy2)1/2 (3)
The direction of motion at any point after time t is given by the equation:
Direction of motion after time t tanθ = vy/vx (4)
where θ is the
angle that the trajectory makes with the horizontal at that point.
Example problems
A ball is thrown horizontally with an initial velocity of 6 ms-1 from an open window that is 4m above the ground. Calculate:
(a) the time it takes to hit the ground
(b) the distance from the wall where it hits the ground
(c) the velocity (magnitude and direction 0.5 seconds after it is thrown.
(Ignore air resistance in your calculations and take g = 9.8 ms-2).
(a) Using h = ½ gt2 4 = ½x9.8xt2 and so
t = 0.904 s = 0.90 s
(b) Using s = vt = 6x0.904 = 5.42 m
(c) Vertical velocity after 0.5 s = 0 + gt = 9.8x0.5 = 4.9 ms-1
Velocity after 0.5s = [4.92 + 62]1/2 = 7.75 ms-1
Direction of motion: tan θ = 4.92/6 = 0.82 and so
θ = 39.4o
Combining equations (1) and (2) we can get an
equation for the path as a whole.
From (1) t = s/u and substituting this in (2) we have:
The vertical distance travelled (h) = ½(gt2 = ½(gs2/u2) = s2[½(g/u2)] (5)
so h is proportional to
s2 and this is the equation of a parabola. All objects projected through gravitational
fields travel in parabolas if we ignore the effects of air resistance.
The time taken for the
object to reach the ground along the parabolic path is the same as if it were dropped
vertically.
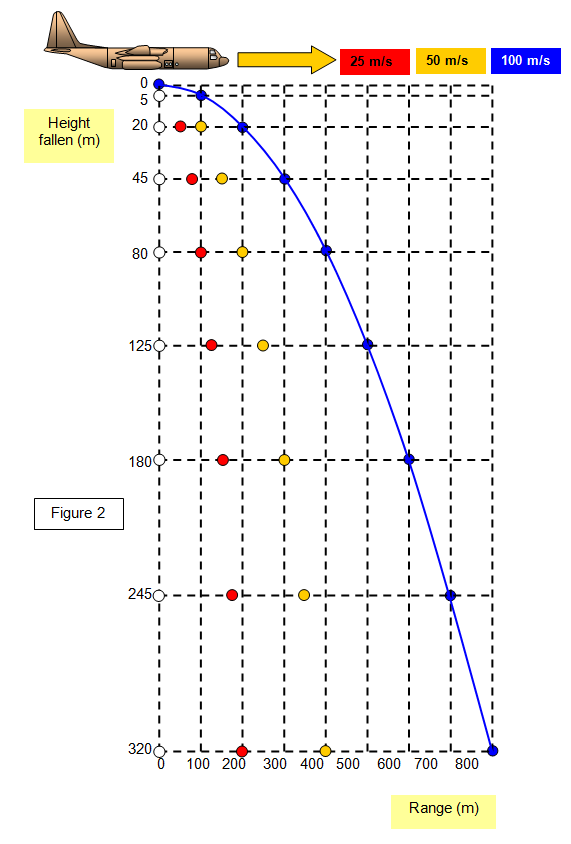
The parabolic path for an object projected horizontally is shown in Figure
2.
Notice that if air resistance is ignored the vertical height of the object at given times
after the start is the same no matter what horizontal velocity it had at the moment of
release.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB