Object projected at an angle
Consider now the case of an object that is
projected at an angle to the horizontal other than 90o.
It is helpful to treat the
horizontal and vertical components of velocity separately. A diagram of the motion is shown in
Figure 1.
Consider an object projected with velocity u at an angle A to the
horizontal.
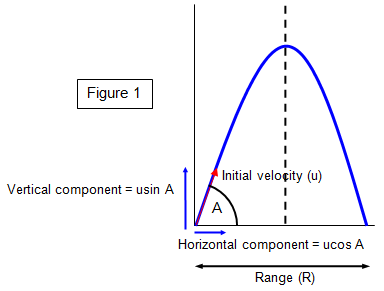
Vertical component of
velocity = a sin A
Horizontal component of velocity = u cos A
If we ignore the effects
of air resistance, the horizontal velocity is constant and the vertical velocity changes with a
uniform acceleration. The path that the body follows is a parabola as can be seen from the proof
below.
Vertical motion: h = ut sin A – ½ gt
2 Horizontal motion: s = ut
cos A
(a) Range
The object will hit the ground again when
h = 0, i.e. when ut sin A = ½ gt
2.
Therefore it will hit the ground after a time t,
where t = 2u sin A/g.
Therefore the range R is given by:
R = horizontal velocity x time
= [ucos A x 2u sin A]/g = [u
2 2 sin A cos A]/g = u
2sin 2A/g
Range = u2sin 2A/g
The maximum range for a given velocity of projection is
when sin 2A = 1, that is, when 2A = 90
o or when A = 45
o
(b)
Height
The projectile will reach its maximum height when the vertical component of its
velocity is zero, that is, when:
u sin A - gt = 0, or t = u sin [A/g]
This gives the maximum
height (H) reached as: H = [u
2sin
2 A]/2g
Maximum height reached H = [u2sin2 A]/2g
Example problem
A stone is projected at an angle of 60o to the horizontal with a velocity of 30 m s-1.
Calculate
(a) the highest point reached,
(b) the range,
(c) the time taken for the flight,
(d) the height of the stone at the instant that the path makes an angle of 30o with the horizontal.
(a) Highest point = 302 sin2 600/2g = 900 x 0.75/20 = 33.75m.
(b)Range = 302 sin 120o/10 = 900x0.866/10 = 78 m.
(c)Time of flight = 2x30sin60o/10 = 5.2 s
(d) At the point when the path makes an angle of 30o to the horizontal we have:
tan 30o = vertical component of velocity/ horizontal component of velocity
= vertical component/30 cos60
The vertical component (v) is given by the formula. v2 =302sin260o - (2x10xh)=(900x 0.75)-20h where h is the height reached at that point.
Therefore tan 30o = [675 - 20h]/15 15 x 0.58 = 675 – 20h 8.66 = 675 - 20h
20h = 666.3 h = 33.3 m
Example problem
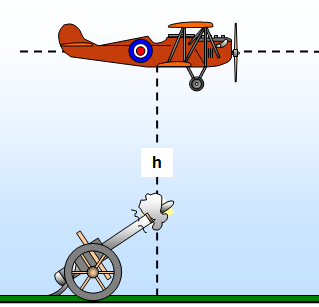
An aeroplane flies at a height h at a constant speed u in a straight horizontal line, so as to pass vertically over a certain gun. At the instant when the aeroplane is directly over it the gun fires a shell which hits the plane.
Find the minimum muzzle velocity (v) of the shell and the correct angle of elevation (A) of the gun at this velocity (neglecting air resistance).
If we require the minimum muzzle velocity, then the height of the plane when it is hit must be the maximum height reached by the shell, in other words the vertical component of its velocity must be zero when it hits the plane.
Therefore 0 = v
2sin
2 A –2gh
Therefore: 0 = v
2(1 - cos
2 A) - 2gh
But u = vcos A
v
2 = u
2+2gh v =(u
2 + 2gh)
1/2 and this gives
tanA = [2gh]
1/2/u
Trajectory – parabolic path
The
shape of the trajectory can be found by combining the equations for vertical and horizontal
velocity.
Taking the vertical displacement as y and the horizontal displacement as x, we have.
x = ut cos A
y = ut sin A – ½ gt
2This gives: y = x tanA –
gx
2/
2u
2 cos
2A
For a given angle of projection (A) and
projection velocity (u), this becomes:
y = Bx - Cx
2where B and C are constants (B = tanA
and C = g/2u
2 cos
2A) ; this is the equation of a parabola.
The above
equations only refer to projectiles where the effects of air resistance have been ignored. Quite
different paths may be found in practice for such objects as golf balls, javelins and discoi.
Student investigation
Make three model car tracks, one straight and two in the shape of a catenary. Try allowing model cars to run down each track and explain what you observe.
Start two cars at different points on the two catenary tracks. Which one gets to the bottom first? Try to explain the results.
A VERSION IN WORD IS AVAILABLE ON THE SCHOOLPHYSICS USB
