Relative velocity

The velocity of an object only really has meaning when it is expressed relative to a set of axes or 'frame of reference'.

We usually consider the motion of objects moving relative to the Earth, but since the Earth is orbiting the Sun and the Sun is moving through the Galaxy this is a purely arbitrary concept. When dealing with more than one body in motion the problem is complex - consider the difficulties in sending the space probe Giotto to rendezvous with Halley's comet many millions of miles away!
We should always specify the frame of reference relative to which an object is moving.

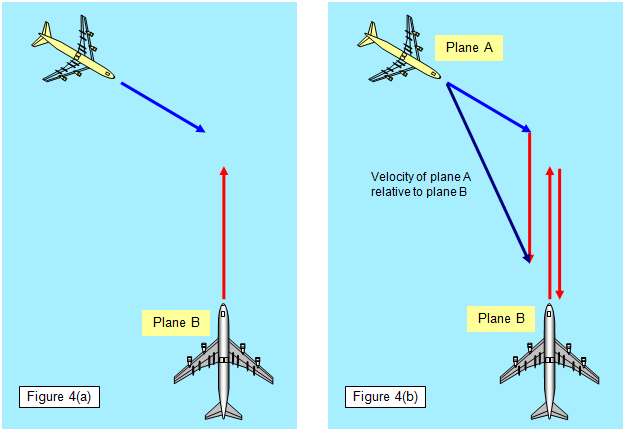
Think about the case where both bodies are moving relative to a third. A simple example would be where the motions of both bodies are in the same straight line - for instance, two cars travelling along a motorway. If both cars are travelling in the same direction, one at 25 ms^-1 and the other at 35 ms^-1 then their relative velocity is 10 ms^-1 (by vector addition).

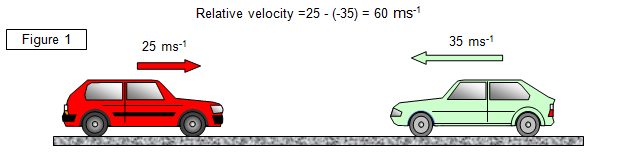
If they are moving in opposite directions, however, the relative velocity of one car with respect to the other is therefore 60ms-1 (See Figure 1).

What we are effectively doing is considering one car to be at rest and finding the velocity of the other car in that frame of reference. To do this we must add the negative of the velocity of one car to both cars' velocities. This effectively brings one to rest and we then consider the velocity of the other car relative to it.

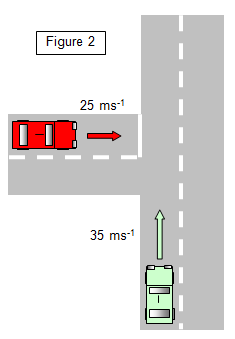
The situation is a little more complex when the motion of the two objects is not in the same straight line. Consider the case shown in Figure 2.

Here the two cars are still moving at the same speeds but this time at right angles to each other as they approach a junction.

The relative velocity is found by using a vector triangle.


If we add the negative of the velocity of the red car (-25) to both the velocity of the red car and the green car we can imagine the red car to be at rest and then find the velocity of the green car relative to it. (See Figure 3).

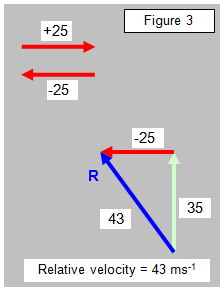
This is most easily done by drawing the vector diagram. The resultant shown by the vector R is the velocity of the green car relative to the red car. In our example the velocity of the green car relative to the red car is 43 ms^-1 and in a direction of 325 ^o.


Think about the result and see if it matches your common sense view of how you would see the green car moving if you were in the red car. It would seem to be moving up the page and towards the left. It does actually fit the result!

Relative motion at angles other than 90^o

We will consider the case where the cars are not moving at right angles to each other.
In fact we will not consider cars at all but the two aeroplanes shown in Figure 4 (a).


To find the velocity of plane A relative to plane B we must 'make plane B stationary'. We do this by adding the negative of plane B's velocity to both planes. If we were on plane B it would be like making that plane stop and we would then see plane A moving relative to us. This is done in Figure 4(b).