Angular momentum

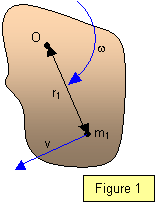
Rotating bodies show the same reluctance to a change in their angular velocity as bodies moving in a straight line do to a change in their linear velocity. This is due to a property of the object known as its angular momentum. A body can possess angular momentum as you can see from Figure 1.

Consider a particle of the body of mass m₁ rotating at a distance r₁ from the centre of rotation (O); its linear momentum at that instant is m₁v₁ = m₁r₁w, where w is the angular velocity of the body.


Therefore the angular momentum of m₁ is: = r₁(m₁r₁w) = m₁w r₁².

If we add together the angular momentum for all the particles of the body then:
angular momentum of the body = Smwr² = wSmr² = Iw


The units for angular momentum are kg m² radian s^-1

You should have expected a result like this, as it is similar to that for linear momentum (mu). (I taking the place of m and w taking the place of u)

In the same way that if a force is applied to a body for a certain time it will change the linear momentum of a body the application of a couple C for a certain time t will change the angular velocity from w_o to w₁ and so give a change of angular momentum of the body such that:

Radius of gyration

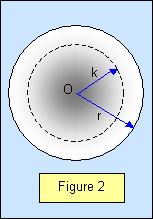
A useful term when considering rotating objects is one known as the radius of gyration. We can write the moment of inertia I of a body as Mk²₁ where M is the mass of the body and k is a distance called the radius of gyration of the body. For example, for a disc the moment of inertia is Mr²/2, and so k = (r²/2)^1/2 = r/2^1/2 .
(see Figure 2).

The radius of gyration can be defined as the distance from the centre of rotation of a rotating body to the point where the mass can be considered to be concentrated (not to be confused with the centre of mass).

Conservation of angular momentum

In the same way that linear momentum is conserved in a collision angular momentum is conserved in an isolated system where no external couples act.

The angular momentum of an isolated system is constant.

This may be expressed in a formula as:


where Iw_o and Iw₁ are the initial and final angular momenta of the system.


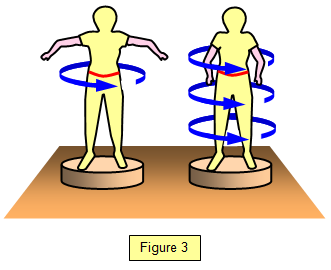
A very simple demonstration of this law can be shown by a person standing on a rotating platform. If they first rotate with their arms outstretched and then bring their arms in, their angular velocity will increase. (Figure 3).

This happens because their angular momentum must remain constant, the decrease in their moment of inertia as they drop their arms results in an increase in their angular velocity. The effects are much more impressive if the person holds a heavy book or a 1 kg mass in each hand.

Many of you will have experienced the effects of the conservation of angular momentum when riding a bike. It is very hard to keep the bike upright when it is stationary, but as soon as the bike is moving and its wheels are rotating it becomes much easier.

The rotation of the wheels produces angular momentum and prevents the bike from falling sideways, because this would give a change in the angular momentum (since this is a vector quantity).

A helicopter is prevented from rotating about a vertical axis either by the small tail rotor or by a sideways jet of air ducted through the tail boom.