Couples and angular acceleration
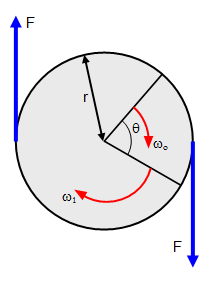
In just the same way that a body's linear velocity can be changed by the
application of a force for a time t its angular velocity can be changed by a couple (Fd) acting
on it for a time t.
If a couple is applied for a time t as shown in the diagram, the
angular velocity of the body will be changed from ω
o to ω
1 this means the body experiences
an angular acceleration (α).
Suppose that the body rotates through an angle θ
during the acceleration. We can then write down three equations for the motion:
θ = ω
ot
+ ½ αt
2ω
12 = ω
o2 + αθ
ω = [ω
1 – ω
o]/t
The work done by the couple is given
by the equation:
Work done = Tθ = F x 2r x 2πn = 4πnrF
where r is the distance of one of the
forces from the axis of rotation and n is the number of rotations. The angle through which the
body has rotated during the acceleration is 2πn.
If a continuous input of energy is
required to maintain a constant angular velocity ω against a frictional couple T then:
Energy used per second = power = θ/t = Tω
So applying a torque
to a body of a certain moment of inertia will change its angular acceleration. The torque T,
the moment of inertia I and the angular acceleration
a are related by the equation:
Torque (T) = Iα
Example problems
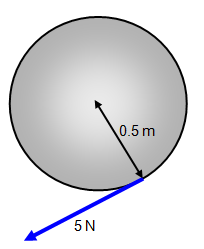
A force of 5 N is applied for 3 s to the rim of stationary wheel of mass 4 kg and radius 0.5 m.
Calculate:
(a) the angular acceleration
(b) the final angular velocity
(c) the number of revolutions in that time
(d) the energy gained by the wheel
(e) the work done by the couple
(a) C = Iα
5 x 0.5 = (4 x 0.5
2α/2
angular acceleration (α) = 5 rad s
-2
(b) α
1 = ω
o + ωt = 0 + 5 x 3 = 15 rad s
-1.
(c) Average velocity = 7.5 rad s
-1.
Therefore in 3s the wheel turns through = 3 x 7.5 = 22.5 rads
Therefore number of revs = 22.5/2π = 3.58.
(d) Energy gained = ½ ω
2 = 0.5 x 0.5 x 15 x 15 = 56.25 J.
(e) Work done = 4πnrF = 5 x 2
p x 2 x 0.5 x 3.58 = 112.5 J.
