
Forced vibrations can also show another very important effect. With the
swing you will find that if you push in time with the natural frequency of the swing then the
oscillations build up rapidly. This last fact is an example of resonance.
All systems have their own natural frequency, and if you apply a
driving force of the same frequency and in phase with the initial oscillations then resonance
results, the amplitude of the oscillations gets larger and larger. Parts of a car may vibrate if you
drive over a bumpy road at a speed where the vibrations transmitted to the body are at the
resonant frequency of that apart. (Actually cars are designed not to do this by choosing parts
with natural frequencies that are not likely to be produced by driving). Bass frequencies from
stereo speakers can make a room resonate, particularly annoying if you live next door and your
living room resonates due to your neighbour's music!
When I was a teenager on my way to
school I used to go across a small suspension bridge and if I timed my footsteps at a particular
rate I could make the bridge swing! A classic and rather unfortunate example of this was the
Millennium Bridge built across the River Thames in London. However the most alarming exam-
ple of the effect of resonance on a suspension bridge was when the Tacoma Narrows
suspension bridge collapsed in a gale, due to resonance. The rebuilt bridge was redesigned to
limit the amplitude of horizontal oscillation and is now safe!
Barton's pendulums
(Figure 1) are a very good way of demonstrating forced vibrations and resonance in the
laboratory. A heavy driving pendulum X is hung from a thread fixed to a cord between two retort
stands. Hanging from the cord are five other pendulums, each with a light paper cone as the
bob.
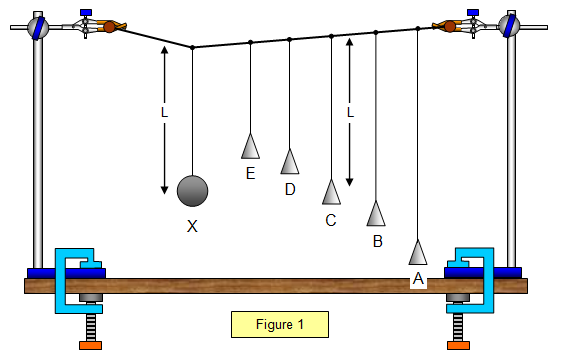
As X is swung all
the other pendulums begin to vibrate, but pendulum C has the greatest amplitude as it has the
same length and therefore the same natural frequency as X.
It is found that:
A
and B are about half a period behind X
C is about a quarter of a period behind X
D and
E are nearly in phase with X.
The effects of resonance can be demonstrated in several areas of Physics.
You may find that the internal mirror in a car vibrates strongly when travelling at one particular
speed over a rough road. If a cello is played near a piano, the sounding of the cello note may
make a string of the same frequency on the piano resonate. The breaking of a wine glass by a
loud note of a particular frequency is also due to this effect. The absorption of light by a gas
depends on a resonance effect within the atom and the tuned LCR circuit resonates at one
particular frequency. Microwave ovens operate at a frequency of 2.45 GHz (2.45x109 Hz) and
this is NOT the resonant frequency of a water molecule. This frequency is much lower than the
diatomic molecule resonant frequencies mentioned earlier. If 2.45 GHz were the resonant
frequency of water molecules the microwaves would all be absorbed in the surface layer of a
substance (liquid water or food) and so the interior of the food would not get cooked at
all.
The variation of amplitude of the system with input frequency is shown in Figure 2.
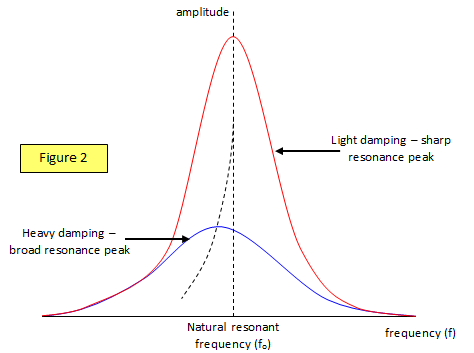
No mechanical system
will vibrate at only its resonant frequency. The actual dependence of the amplitude of the
system on the frequency of the driving force varies over a range of frequencies near the
resonant frequency and this variation known as a resonance curve. The amount of damping of a
system affects the shape of the resonance curve. Two examples of this variation are shown in
Figure 2. One is for light damping (the oscillations of a tuning fork) and the other for heavy
damping (the oscillations of the air in a bottle when you blow across the top). The air can be
made to oscillate over quite a large range of frequencies but the oscillations
are heavily
damped and die away rapidly.
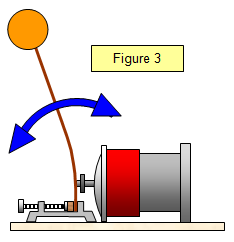
An alternative method
for investigating resonance is to fix a springy metal strip top the top of the vibration generator
and load each end with equal small masses of plasticene. The vibration generator is then turned
on and a resonance frequency found.
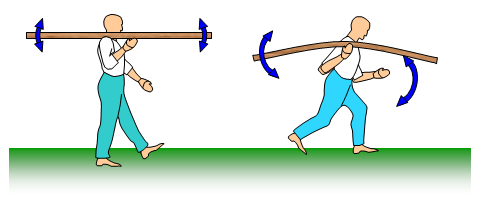
This is similar to the case where a man walks across a field
carrying a long plank on his shoulder. At each step the plank flexes a little (a) and the ends move up and down. He
then starts to trot and as a result bounces up and down (b). At one particular speed resonance will occur between the
motion of the man and the plank and the ends of the plank then oscillate with large amplitude.