You will probably have
noticed that objects in water appear to weigh less then when they are in air. For example if
you try to lift up a weight in a swimming pool and then try to lift the same weight on the edge
of the pool, it feels much lighter in the water.
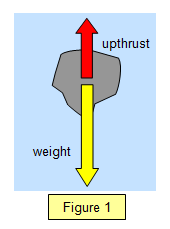
When an object is in a fluid (such as
water) it will displace a certain amount of the fluid. The effect of this is to produce an upward
force on the body and the apparent weight of the body is therefore less in the fluid than it
would be a vacuum (Figure 1). The magnitude of this upward force, or upthrust, depends
on
(a) the volume of the body - the more fluid that is displaced the greater the
upthrust;
(b) the density of the fluid - the greater the density the greater the
upthrust.
Archimedes, a Greek physicist of the third century BC, is said to have been
pondering the problems of flotation while having a bath when he suddenly realised why
objects appear to weigh less when immersed in a denser fluid.
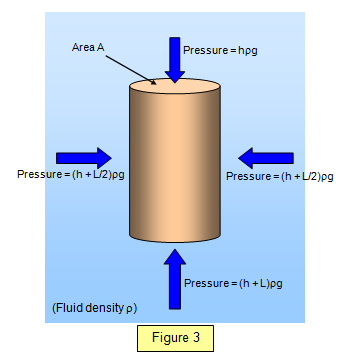
Force on the upper face of the cylinder = hρgA
Force on the lower face of the cylinder = [h + L]ρgA
Difference in force = LρgA
But LA is the volume of liquid displaced by the cylinder,
and LrgA is the weight of the liquid displaced by the
cylinder.
Therefore there is a net upward force on the cylinder equal to the weight of
the fluid displaced by it.
The same result will be obtained for a body of any shape,
regular or not by taking into account the vertical and horirontal
components of the forces on the object.
If a sphere of radius r made of material
of density σ is fully immersed in a liquid of density ρ the apparent weight of the sphere is given by:
Apparent
weight = actual weight - upthrust = 4/3 πr3g(ρ - s)
The fluid may be a liquid,
such as water, or a gas, such as air, although due to the low density of air (about 1 kg m3)
the upthrust in air in usually small, but sufficient to support a helium-filled balloon or a hot air
balloon.
It should be clear from the above that a floating body will displace its own weight of fluid such that there is no vertical resultant force on the body. The volume of the floating object that is below the surface will depend on both the density of the object and that of the fluid in which it is floating.
Find the volume of an iceberg that is below the surface of sea water.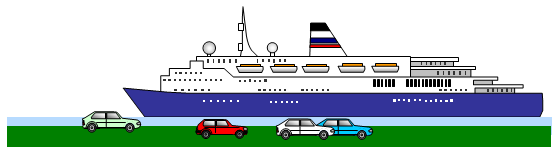
You can use Archimedes principle to get a rough idea of the draught of a ship such as a ferry. In the following example we will consider the Bretagne of the Brittany Ferries fleet that sails across the English Channel between Britain and France.
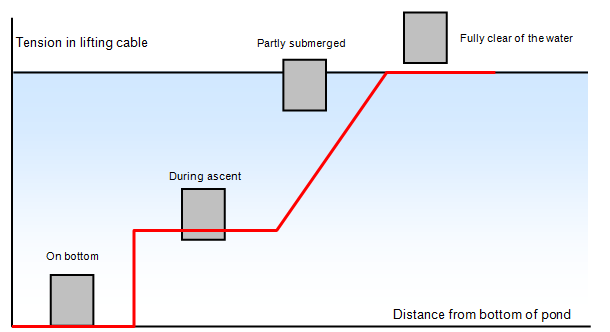
A rectangular block of stone is raised at a constant speed from the bottom of a pond by a crane. Draw the variation in the tension of the cable from the moment the stone leaves the bottom of the pond to when the stone is completely clear of the water.
