
The weight of an object may be taken as acting at one point known as the centre of gravity. You could think of that point as the position where all the mass of the object could be thought to be concentrated.
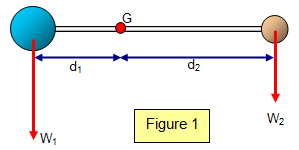
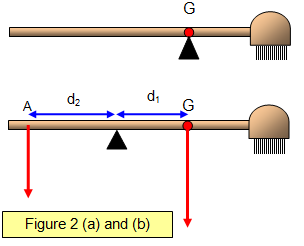 If a broom is balanced on a fulcrum
(Figure 2(a)) its centre of gravity can be found. If it is then balanced on a different point (Figure
2.b) with a known force F using the principle of moments:
If a broom is balanced on a fulcrum
(Figure 2(a)) its centre of gravity can be found. If it is then balanced on a different point (Figure
2.b) with a known force F using the principle of moments:If the gravitational field is uniform over the size of the object then the centre of mass and the centre of gravity of the object will coincide. However if this is not true then they will be in different places. Close to a black hole where the gravitational field changes rapidly might give you a situation like this! This would also mean that a unit mass at one point in an object would have a different force on it from another unit mass somewhere else in the object and so the object would be distorted.
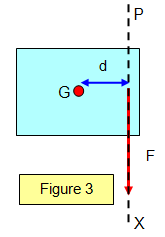
In Figure 3 a force F acts at P. This will do two things:
(a)
cause the box to move along the line PX and
(b) rotate about the centre of gravity
(G)
The moment about G is Fd and so we could
replace the force by an equal one acting through G in the x direction and a couple of moment Fd
about G. This couple could be provided by any size force acting at any distance from G as long
as the product of force and distance was Fd.