Components of vectors

It is often necessary to find the components of a vector, usually in two perpendicular directions. This process is called the resolution of a vector. What you are really doing is finding the effectiveness of the vector along a specified direction.
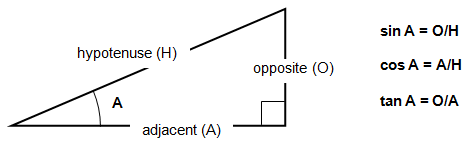
The component of a vector along any direction is the magnitude of the vector multiplied by the cosine of the angle between the vector and the line.

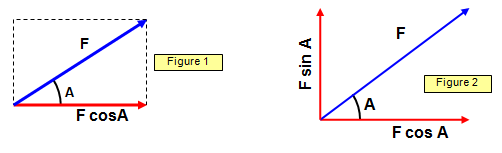
The horizontal component of the vector F shown in Figure 1 is F cos (A) while Figure 2 shows the components of a vector in two perpendicular directions. These are known as the rectangular components of the vector. We call the component of F in the x direction F_x and that in the y direction F_y.

Imagine pulling a barge along a canal or a truck along a track by rope inclined at an angle to the track (Figure 3). The smaller the angle the more effective the force in the rope (the cosine of the angle gets bigger when the angle gets smaller).

The purpose of the following diagrams is to see if you can work out the components of each vector although the diagrams are twisted round at odd angles.



The force in the towrope between a tug and a large liner has both a vertical and a horizontal component.

A projectile

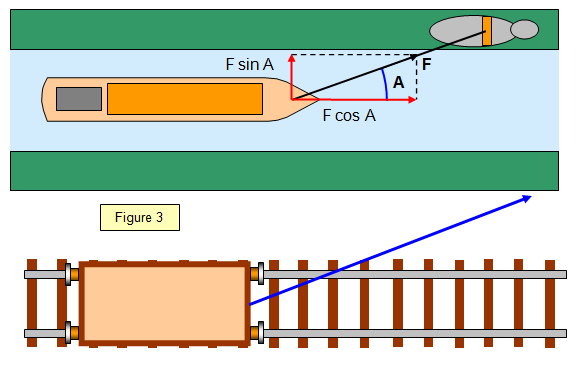
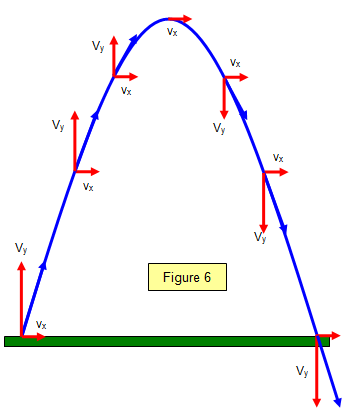
Resolution of vectors is especially useful when considering problems like the motion of a projectile (Figure 6). Its velocity at any point on its path is the combination of a horizontal component (v_x) (constant if there is no air resistance) and a vertical component (v_y) which varies as time goes by. This vertical component is maximum at the bottom of the path and zero at the top.
If A is the angle of projection (relative to the horizontal) and the velocity of projection is u then:

Horizontal component = v_x = u cos A
Initial vertical component = v_y = u sin A

In the diagram the blue vectors represent the actual velocity at any point while the red vectors represent the horizontal and vertical components of these velocities.